题目内容
（2012•菏泽）如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：（1）试证明三角形△ABC为直角三角形；
（2）判断△ABC和△DEF是否相似，并说明理由；
（3）画一个三角形，使它的三个顶点为P1，P2，P3，P4，P5中的3个格点并且与△ABC相似（要求：不写作法与证明）．
分析：（1）利用网格得出AB2=20，AC2=5，BC2=25，再利用勾股定理逆定理得出答案即可；
（2）利用AB=2
，AC=
，BC=5以及DE=4
，DF=2
，EF=2
，利用三角形三边比值关系得出即可；
（3）根据△P2P4 P5三边与△ABC三边长度得出答案即可．
（2）利用AB=2
| 5 |
| 5 |
| 2 |
| 2 |
| 10 |
（3）根据△P2P4 P5三边与△ABC三边长度得出答案即可．
解答：解：（1）∵AB2=20，AC2=5，BC2=25；
∴AB2+AC2=BC2，
根据勾股定理的逆定理得△ABC 为直角三角形；
（2）△ABC和△DEF相似．
由（1）中数据得AB=2
，AC=
，BC=5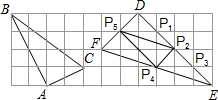
，
DE=4
，DF=2
，EF=2
．
=
=
=
=
，
∴△ABC∽△DEF．
（3）如图：连接P2P5，P2P4，P4P5，
∵P2P5=
，P2P4=
，P4P5=2
，
AB=2
，AC=
，BC=5，
∴
=
=
=
，
∴，△ABC∽△P2P4 P5．
∴AB2+AC2=BC2，
根据勾股定理的逆定理得△ABC 为直角三角形；
（2）△ABC和△DEF相似．
由（1）中数据得AB=2
| 5 |
| 5 |
，DE=4
| 2 |
| 2 |
| 10 |
| AB |
| DE |
| AC |
| DF |
| BC |
| EF |
| ||
2
|
| ||
| 4 |
∴△ABC∽△DEF．
（3）如图：连接P2P5，P2P4，P4P5，
∵P2P5=
| 10 |
| 2 |
| 2 |
AB=2
| 5 |
| 5 |
∴
| P2P5 |
| BC |
| P4P5 |
| AB |
| P2P4 |
| AC |
| ||
| 5 |
∴，△ABC∽△P2P4 P5．
点评：此题主要考查了相似三角形的判定以及勾股定理与逆定理应用，根据已知得出三角形各边长度是解题关键．
练习册系列答案
相关题目
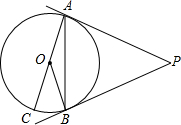（2012•菏泽）如图，PA，PB是⊙O是切线，A，B为切点，AC是⊙O的直径，若∠P=46°，则∠BAC=
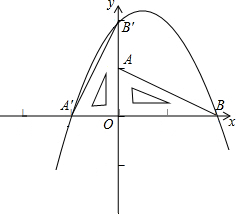将此三角板绕原点O逆时针旋转90°，得到△A′B′O．
