题目内容
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以线段
,以线段![]() 为边在第一象限作等边
为边在第一象限作等边![]() .
.
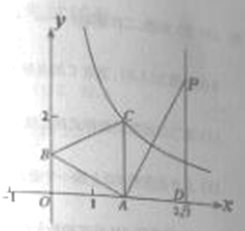
(1)若点![]() 在反比例函数
在反比例函数![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点![]() 在第一象限,过点
在第一象限,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,当
,当![]() 与
与![]() 相切时,
相切时,![]() 点是否在(1)中反比例函数图象上,如果在,求出
点是否在(1)中反比例函数图象上,如果在,求出![]() 点坐标;如果不在,请加以说明.
点坐标;如果不在,请加以说明.
【答案】(1)![]() ;(2)存在,(2
;(2)存在,(2![]() ,1).
,1).
【解析】
试题分析:(1)由直线解析式可求得A、B坐标,在Rt△AOB中,利用三角函数定义可求得∠BAO=30°,且可求得AB的长,从而可求得CA⊥OA,则可求得C点坐标,利用待定系数法可求得反比例函数解析式;
(2)分△PAD∽△ABO和△PAD∽△BAO两种情况,分别利用相似三角形的性质可求得m的值,可求得P点坐标,代入反比例函数解析式进行验证即可.
试题解析:(1)在![]() 中,令y=0可解得x=
中,令y=0可解得x=![]() ,令x=0可得y=1,
,令x=0可得y=1,
∴A(![]() ,0),B(0,1),∴tan∠BAO=
,0),B(0,1),∴tan∠BAO=![]() ,∴∠BAO=30°,
,∴∠BAO=30°,
∵△ABC是等边三角形,∴∠BAC=60°,∴∠CAO=90°,
在Rt△BOA中,由勾股定理可得AB=2,∴AC=2,∴C(![]() ,2),
,2),
∵点C在反比例函数![]() 的图象上,∴k=2×
的图象上,∴k=2×![]() =2
=2![]() ,
,
∴反比例函数解析式为![]() ;
;
(2)∵P(2![]() ,m)在第一象限,∴AD=OD﹣OA=2
,m)在第一象限,∴AD=OD﹣OA=2![]() ﹣
﹣![]() =
=![]() ,PD=m,
,PD=m,
当△ADP∽△AOB时,则有![]() ,即
,即![]() ,解得m=1,此时P点坐标为(2
,解得m=1,此时P点坐标为(2![]() ,1);
,1);
当△PDA∽△AOB时,则有![]() ,即
,即![]() ,解得m=3,此时P点坐标为(2
,解得m=3,此时P点坐标为(2![]() ,3);
,3);
把P(2![]() ,3)代入
,3)代入![]() 可得
可得![]() ,∴P(2
,∴P(2![]() ,3)不在反比例函数图象上,
,3)不在反比例函数图象上,
把P(2![]() ,1)代入反比例函数解析式得
,1)代入反比例函数解析式得![]() ,∴P(2
,∴P(2![]() ,1)在反比例函数图象上;
,1)在反比例函数图象上;
综上可知P点坐标为(2![]() ,1).
,1).

练习册系列答案
相关题目


