题目内容
【题目】如图,P是△ABC内一点,
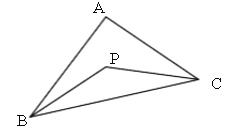
(1)求证:∠BPC>∠A
(2)若∠A=100°,∠ABP=25°,∠ACP=20°求∠BPC的度数。
【答案】(1)证明见解析;(2)∠BPC=145°.
【解析】试题分析:(1)延长BP交AC于M,根据三角形外角大于任意不相邻的内角可得∠BPC>∠PMC,∠PMC>∠A,即可得到结论;
(2)根据三角形外角定理可得∠BPC=∠PMC+∠PCM,∠PCM=∠A+∠ABP,即可解决.
试题解析:(1)延长BP交AC于M,
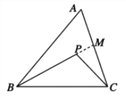
∵∠BPC是三角形PMC的外角,
∴∠BPC>∠PMC,
∵∠PMC是三角形ABM的外角,
∴∠PMC>∠A,
∴∠BPC>∠A;
(2)由(1)知,∵∠PMC是三角形ABM的外角,
∴∠PMC=∠A+∠ABM=100°+25°=125°,
∵∠BPC是三角形POC的外角,
∴∠BPC=∠PMC+∠ACP=125°+20°=145°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目