题目内容

【题目】如图，平行四边形ABCD的周长是18 cm，其对角线AC，BD相交于点O，过点O的直线分别与AD，BC相交于点E，F，且OE=2 cm，则四边形CDEF的周长是_______．

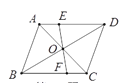
【答案】13cm

【解析】

利用平行四边形的性质得出AO=CO，AD∥BC，进而得出∠EAC=∠FCO，再利用ASA求出△AOE≌△COF，即可得出答案．

解：∵平行四边形ABCD的对角线AC，BD交于点O，

∴AO=CO，AD∥BC，

∴∠EAC=∠FCO，

在△AOE和△COF中，

∠EAO＝∠FCO，AO＝CO，∠AOE＝∠COF，

∴△AOE≌△COF（ASA），

∴AE=CF．

∴四边形CDEF的周长=CD+CF+EF+ED=CD+AD+2OE=9+4=13cm，

故答案为：13cm

练习册系列答案
相关题目

【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

（1）证明与推断：

①求证：四边形CEGF是正方形；

②推断：的值为　 　：

（2）探究与证明：

将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

（3）拓展与运用：

正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

【题目】如图，正方形OABC的边长为6，A，C分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y＝的图象经过点Q，若S△BPQ＝S△OQC，则k的值为___．

【题目】如图，在矩形纸片ABCD中，BM，DN分别平分∠ABC，∠CDA，沿BP折叠，点A恰好落在BM上的点E处，延长PE交DN于点F沿DQ折叠，点C恰好落在DN上的点G处，延长QG交BM于点H，若四边形EFGH恰好是正方形，且边长为1，则矩形ABCD的面积为____．

【题目】如图1，在平面直角坐标系内，A，B为x轴上两点，以AB为直径的⊙M交y轴于C，D两点，C为的中点，弦AE交y轴于点F，且点A的坐标为（2，0），CD＝8

（1）求⊙M的半径；

（2）动点P在⊙M的圆周上运动．

①如图1，当FP的长度最大时，点P记为P，在图1中画出点P0，并求出点P0横坐标a的值；

②如图1，当EP平分∠AEB时，求EP的长度；

③如图2，过点D作⊙M的切线交x轴于点Q，当点P与点A，B不重合时，请证明为定值．

【题目】如图，直线y =x与反比例函数y =（x＞0）的图象交于点A，已知点A的横坐标为4．

（1）求反比例函数的解析式；

（2）将直线y =x向上平移3个单位后的直线l与y =（x＞0）的图象交于点C；

①求点C的坐标；

②记y =（x＞0）的图象在点A，C之间的部分与线段OA，OC围成的区域（不含边界）为W，则区域W内的整点（横，纵坐标都是整数的点）的个数为 .

【题目】如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．

（1）求二次函数的解析式；

（2）根据图象直接写出使一次函数值大于二次函数值的x的取值范围；

（3）若直线与y轴的交点为E，连结AD、AE，求△ADE的面积．

【题目】正方形ABCD的边长为1，点O是BC边上的一个动点（与B，C不重合），以O为顶点在BC所在直线的上方作∠MON=90°

（1）当OM经过点A时，

①请直接填空：ON______（可能，不可能）过D点：（图1仅供分析）

②如图2，在ON上截取OE=OA，过E点作EF垂直于直线BC，垂足为点F，作EH⊥CD于H，求证：四边形EFCH为正方形；

③如图2，将②中的已知与结论互换，即在ON上取点E（E点在正方形ABCD外部），过E点作EF垂直于直线BC，垂足为点F，作EH⊥CD于H，若四边形EFCH为正方形，那么OE与OA是否相等？请说明理由；

（2）当点O在射线BC上且OM不过点A时，设OM交边AB于G，且OG=2．在ON上存在点P，过P点作PK垂直于直线BC，垂足为点K，使得S△PKO=S△OBG，连接GP，则当BO为何值时，四边形PKBG的面积最大？最大面积为多少？

【题目】已知关于x的方程x2+（m﹣3）x﹣m（2m﹣3）=0

（1）证明：无论m为何值方程都有两个实数根；

（2）是否存在正数m，使方程的两个实数根的平方和等于26？若存在，求出满足条件的正数m的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网