Question

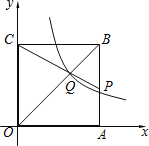
【题目】如图，正方形OABC的边长为6，A，C分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y＝的图象经过点Q，若S△BPQ＝S△OQC，则k的值为___．

Answer 1

【答案】16

【解析】

根据正方形的性质可得出OC∥AB，从而得出△BPQ∽△OCQ，再根据S△BPQ＝S△OCQ，即可得出点P的坐标，利用待定系数法求出直线OB、CP的解析式，联立两个解析式求出交点坐标后再由反比例函数图象上点的坐标特征即可得出结论．

∵四边形OABC为正方形，

∴OC∥AB，

∴△BPQ∽△OCQ，

∵S△BPQ=S△OCQ，

∴BP=AB.

∵正方形OABC的边长为6，

∴点C(0,6),B(6,6),P(6,3)，

利用待定系数法可求出：

直线OB的解析式为y=x,直线CP的解析式为

联立OB、CP的解析式得：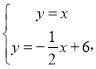

解得：

∴Q(4,4).

∵函数y=的图象经过点Q，

∴k=4×4=16.

故答案为：16.