题目内容
【题目】某校为了解九年级学生的身体素质情况,随机对九年级的50名学生进行一分钟跳绳次数测验,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | a |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a+10 |
第5组 | 160≤x<180 |
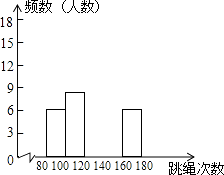
请结合图表完成以下问题.
(1)求出表中的a;
(2)补全频数分布直方图;
(3)若x≥140为优良,该校九年级有450名学生,请估计跳绳成绩达到优良的学生约有多少人?
【答案】
(1)解:观察条形图可知第五组的人数=6人,
根据总人数为50,可得6+a+12+a+10+6=50,
解得a=8.
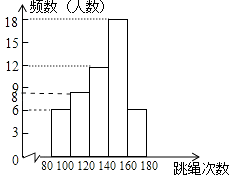
(2)解:频数分布直方图为:
(3)解:估计跳绳成绩达到优良的学生约有) ![]() ×450=216(人).
×450=216(人).
答:估计跳绳成绩达到优良的学生约有216人.
【解析】(1)由频数之和为50可列出方程,求出a;(3)样本的特性可以估计总体的特性,样本的百分比也可以估计总体的相应百分比.
【考点精析】通过灵活运用频数分布直方图,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)即可以解答此题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目