题目内容
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 . 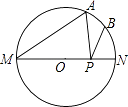
【答案】2 ![]()
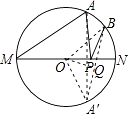
【解析】解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴ ![]() =
= ![]() ,
,
∵∠AMN=40°,
∴∠A′ON=80°,∠BON=40°,
∴∠A′OB=120°,
过O作OQ⊥A′B于Q,
在Rt△A′OQ中,OA′=2,
∴A′B=2A′Q=2 ![]() ,
,
即PA+PB的最小值2 ![]() .
.
所以答案是:2 ![]() .
.
【考点精析】本题主要考查了圆心角、弧、弦的关系的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半才能正确解答此题.

【题目】嘉淇同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比实验.在同等情况下,把稍高于室温(25.5℃)的水放入凉壶中,每隔一小时同时测出凉壶水温,所得数据如下表:
刚倒入时 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
泥茶壶 | 34 | 27 | 25 | 23.5 | 23.0 | 22.5 | 22.5 | 22.5 |
塑料壶 | 34 | 30 | 27 | 26.0 | 25.5 | 22.5 | 22.5 | 22.5 |
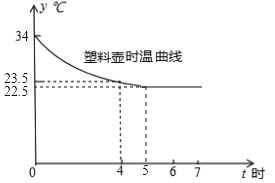
(1)塑料壶水温变化曲线如图,请在同一坐标系中,画出泥壶水温的变化曲线;
(2)比较泥壶和塑料壶水温变化情况的不同点.
【题目】某校为了解九年级学生的身体素质情况,随机对九年级的50名学生进行一分钟跳绳次数测验,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | a |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a+10 |
第5组 | 160≤x<180 |
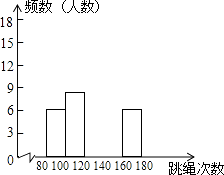
请结合图表完成以下问题.
(1)求出表中的a;
(2)补全频数分布直方图;
(3)若x≥140为优良,该校九年级有450名学生,请估计跳绳成绩达到优良的学生约有多少人?