题目内容
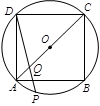
如图,AB是⊙O的直径,C、P是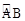 上两点,AB=13,AC=5,
上两点,AB=13,AC=5,
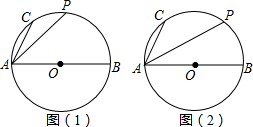
(1)如图(1),若点P是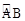 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是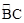 的中点,求PA得长 .
的中点,求PA得长 .
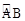 上两点,AB=13,AC=5,
上两点,AB=13,AC=5,(1)如图(1),若点P是
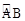 的中点,求PA的长;
的中点,求PA的长;(2)如图(2),若点P是
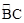 的中点,求PA得长 .
的中点,求PA得长 .
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得.
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
试题解析::(1)如答图(1),连接PB,
∵AB是⊙O的直径且P是
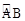 的中点,∴∠PAB=∠PBA=45°,∠APB=90°.
的中点,∴∠PAB=∠PBA=45°,∠APB=90°.又∵在等腰三角形△ABC中有AB=13,
∴
 .
.
(2)如答图(2),连接BC,与OP相交于M点,作PH⊥AB于点H,
∵P点为
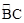 C的中点,∴OP⊥BC,∠OMB=90°,
C的中点,∴OP⊥BC,∠OMB=90°,又∵AB为直径,∴∠ACB=90°.∴∠ACB=∠OMB. ∴OP∥AC.∴∠CAB=∠POB.
又∵∠ACB=∠OHP=90°,∴△ACB∽△0HP.∴
 .
.又∵
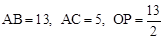 ,∴
,∴ ,解得
,解得 .
.∴AH=OA+OH=9.
∵在Rt△OPH中,有
 。
。∴在RT△AHP中 有
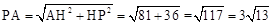 .
.∴PA=
 .
.

练习册系列答案
相关题目
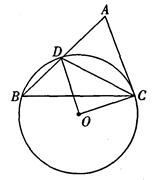
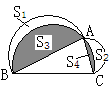
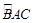 ,如图所示,若AB=4,AC=2,
,如图所示,若AB=4,AC=2,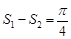 ,则S3-S4的值是( )
,则S3-S4的值是( )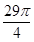
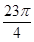
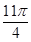
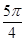
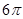
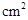
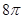
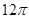

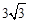
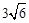
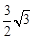
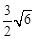
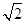 ,则∠BAC的度数是()
,则∠BAC的度数是() 的值为( )
的值为( )