Question

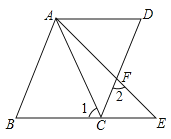
【题目】如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE＝BF，连接DE，过点E作EG⊥DE，使EG＝DE，连接FG，FC.

(1)请判断：FG与CE的数量关系是__________，位置关系是__________；

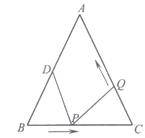
(2)如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，(1)中结论是否仍然成立？请出判断判断并给予证明．

Answer 1

【答案】(1) FG＝CE，FG∥CE；(2)成立，理由见解析.

【解析】

(1)结论：FG＝CE，FG∥CE，如图1中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可；

(2)结论仍然成立，如图2中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可．

(1)结论：FG＝CE，FG∥CE.

理由：如图1中，设DE与CF交于点M，

∵四边形ABCD是正方形，

∴BC＝CD，∠ABC＝∠DCE＝90°，

在△CBF和△DCE中，，

∴△CBF≌△DCE，

∴∠BCF＝∠CDE，CF＝DE，

∵∠BCF＋∠DCM＝90°，

∴∠CDE＋∠DCM＝90°，

∴∠CMD＝90°，

∴CF⊥DE，

∵GE⊥DE，

∴EG∥CF，

∵EG＝DE，CF＝DE，

∴EG＝CF，

∴四边形EGFC是平行四边形．

∴GF＝EC，

∴GF＝EC，GF∥EC.

故答案为FG＝CE，FG∥CE；

(2)结论仍然成立．

理由：如图2中，设DE与CF交于点M，

∵四边形ABCD是正方形，

∴BC＝CD，∠ABC＝∠DCE＝90°，

在△CBF和△DCE中，，

∴△CBF≌△DCE，

∴∠BCF＝∠CDE，CF＝DE，

∵∠BCF＋∠DCM＝90°，

∴∠CDE＋∠DCM＝90°，

∴∠CMD＝90°，

∴CF⊥DE，

∵GE⊥DE，

∴EG∥CF，

∵EG＝DE，CF＝DE，

∴EG＝CF，

∴四边形EGFC是平行四边形．

∴GF＝EC，

∴GF＝EC，GF∥EC.