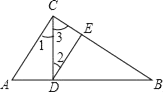
题目内容
【题目】已知AD∥BE,∠B=∠D.
(1)求证:AB∥CD;
(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠DCE的度数.
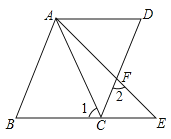
【答案】(1)见解析;(2)75°
【解析】
(1)根据平行线的性质和判定解答即可;
(2)根据平行线的性质得到∠BAC+∠CAE=60°,设∠CAE=x,∠DAE=y,根据题意得到二元一次方程组求出x,y即可求解.
(1)∵AD∥BE,
∴∠D=∠DCE,
∵∠B=∠D,
∴∠DCE=∠B,
∴AB∥CD,
(2)∵AD∥BE,∠1=60°,
∴∠CAE+∠DAE=60°,
∵AB∥CD,∠2=60°,
∴∠BAC+∠CAE=60°,
∵∠BAC=3∠EAC,
设∠CAE=x,∠DAE=y,
可得:![]() ,
,
解得:![]() ,
,
即∠CAE=15°,∠DAE=45°,
∴∠D=180°60°45°=75°,
∴∠DCE=75°.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目