题目内容
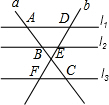如图，l1∥l2∥l3，直线a与l1、l2、l3分别交于A、B、C，直线b与l1、l2、l3分别交于D、E、F，AC=12，DE=5，EF=7，则BC=分析：先根据平行线分线段成比例定理求出AB：BC的比值，再根据AC=12即可求解．
解答：解：∵l1∥l2∥l3，
∴
=
，
∵DE=5，EF=7，
∴
=
，
∵AC=12，
∴BC=12×
=7．
故答案为：7．
∴
| AB |
| BC |
| DE |
| EF |
∵DE=5，EF=7，
∴
| AB |
| BC |
| 5 |
| 7 |
∵AC=12，
∴BC=12×
| 7 |
| 5+7 |
故答案为：7．
点评：本题主要考查了平行线分线段成比例定理，熟记定理找准对应线段是解题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
13、如图，l1∥l2，∠1=120°，∠2=100°，则∠3=（ ）
如图，l1∥l2，AB⊥AC，∠ABC=50°，则∠1=（ ）度．
如图，l1∥l2∥l3，已知L1与l3之间的距离为8cm，l1与l2之间的距离为3cm，则l2与l3之间的距离为
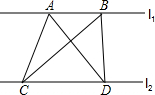如图，l1∥l2，A、B为直线l1上两点，C、D为直线l2上两点，则△ACD与△BCD的面积大小关系是（ ）| A、S△ACD＜S△BCD | B、S△ACD=S△BCD | C、S△ACD＞S△BCD | D、不能确定 |