Question

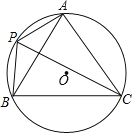
【题目】如图：A、P、B、C是⊙O上的四个点，且∠APC＝∠CPB＝60°

（1）判定△ABC的形状，证明你的结论；

（2）若⊙O的半径为2，求AB的长．

Answer 1

【答案】（1）△ABC是等边三角形，理由见解析；（2）2．

【解析】

（1）根据同弦对应的圆周角相等，可知∠CAB＝∠CPB＝60°，再根据三角形内角和为180°，继而得出△ABC为等边三角形.

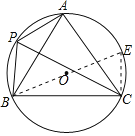
（2）延长BO交⊙O于E，连接CE，可知∠E＝∠BAC＝60°，根据△BEC为直角三角形，可得BE和BC的长.

解：（1）△ABC是等边三角形，

理由如下：由圆周角定理得，∠ABC＝∠APC＝60°，∠CAB＝∠CPB＝60°，

∴△ABC是等边三角形；

（2）延长BO交⊙O于E，连接CE，

由圆周角定理得，∠E＝∠BAC＝60°，

∴，

∴，

∴AB＝BC＝．