Question

【题目】阅读下列材料，回答问题.

材料：求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型，此类题型试题有时出题者将圆隐藏，故又称为“隐圆问题”.解决这类问题，关键是要找到动点的运动轨迹，即该动点是绕哪一个定点旋转，且能保持旋转半径不变.从而找到动点所在的隐藏圆，进面转换成圆外一点到圆心的距离减半径，求得最小值.

解决问题：

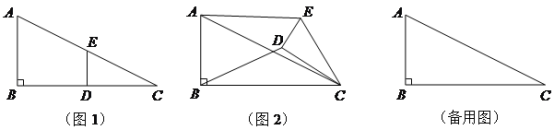
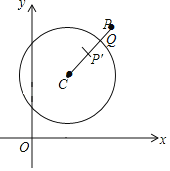
（1）如图①，圆O的半径为1，圆外一点A到圆心的距离为3，圆上一动点B，当A、O、B满足条件____________时，有最小值为____________.

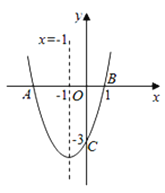
（2）如图②，等腰两腰长为5，底边长为6，以A为圆心，2为半径作圆，圆上动点P到的距离最小值为__________.

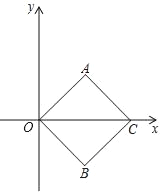
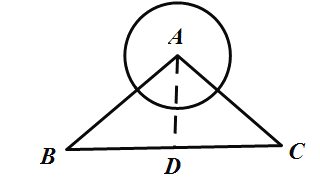
（3）如图③，，P、Q分别是射线、上两个动点，C是线段的中点，且，则在线段滑动的过程中，求点C运动形成的路径长，并说明理由.

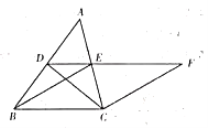
（4）如图④，在矩形中，，，点E是中点，点F是上一点，把沿着翻折，点B落在点处，求的最小值，并说明理由.

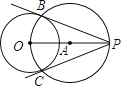
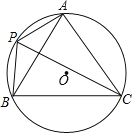
（5）如图⑤，在中，，，，以边中点O为圆心，作半圆与相切，点P，Q分别是边和半圆上的动点，连接，求长的最小值，并说明理由.

Answer 1

【答案】（1）A，B，O在一条直线上（或）；2；（2）2；（3），见解析；（4），见解析；（5）1，见解析.

【解析】

（1）根据最小距离等于圆外一点到圆心的距离减去半径可得到最小值，这时A，B，O在一条直线上；

（2）作AD⊥BC于点D，利用等腰三角形的性质及勾股定理求出AD的长度，用AD的长度减去半径即为圆上动点P到的距离最小值；

（3）根据点C与点O之间的距离永远不变说明点C的运动轨迹为圆，利用弧长公式求路径长即可；

（4）先根据EB为定值，确定点B’的运动轨迹，然后当D,B’,E三点共线时，DB’最小，利用勾股定理求出DE的长度，再减去半径即可；

（5）过O点作，利用三角形中线的性质得出OP,OQ 的长度，从而求出PQ的最小值.

（1）根据最小距离等于圆外一点到圆心的距离减去半径可得到最小值，有最小值为3-1=2此时A，B，O在一条直线上（或）；

（2）如图，作AD⊥BC于点D

∵

由勾股定理得

点P到的距离最小值为

（3）如图，连接，

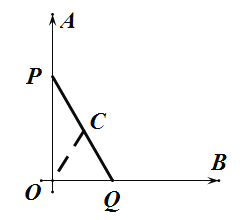
∵，C是中点，，∴所以C是以O为圆心，半径为2的圆上，所以

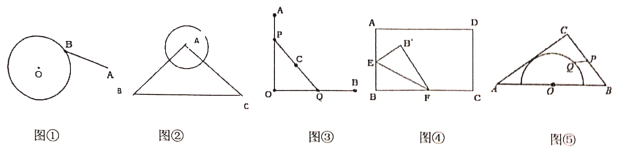
（4）如图，连接DE

因为点E是定点，，所以的轨迹为以E为圆心，2为半径的圆上.，∴的最小值为

（5）如图，过O点作，交圆O于点Q，

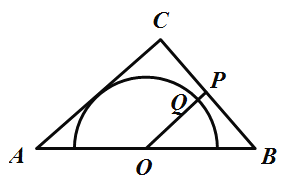
由三角形中线的性质得，，所以最小值为1