题目内容
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
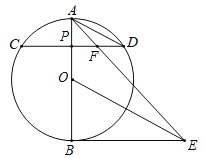
【答案】(1)证明见解析;(2)2;(3)PF=FD,证明见解析.
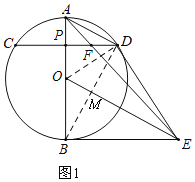
【解析】(1)如图1,连接OD、BD,根据圆周角定理得:∠ADB=90°,则AD⊥BD,OE⊥BD,由垂径定理得:BM=DM,证明△BOE≌△DOE,则∠ODE=∠OBE=90°,可得结论;
(2)设AP=a,根据三角函数得:AD=3a,由勾股定理得:PD=2![]() a,在直角△OPD中,根据勾股定理列方程可得:32=(3-a)2+(2
a,在直角△OPD中,根据勾股定理列方程可得:32=(3-a)2+(2![]() a)2,解出a的值可得AD的值;
a)2,解出a的值可得AD的值;
(3)先证明△APF∽△ABE,得![]() ,由△ADP∽△OEB,得
,由△ADP∽△OEB,得![]() ,可得PD=2PF,可得结论.
,可得PD=2PF,可得结论.
详证明:(1)如图1,连接OD、BD,BD交OE于M,
∵AB是⊙O的直径,
∴∠ADB=90°,AD⊥BD,
∵OE∥AD,
∴OE⊥BD,
∴BM=DM,
∵OB=OD,
∴∠BOM=∠DOM,
∵OE=OE,
∴△BOE≌△DOE(SAS),
∴∠ODE=∠OBE=90°,
∴DE为⊙O切线;
(2)设AP=a,
∵sin∠ADP=![]() ,
,
∴AD=3a,
∴PD=![]() ,
,
∵OP=3-a,
∴OD2=OP2+PD2,
∴32=(3-a)2+(2![]() a)2,
a)2,
9=9-6a+a2+8a2,
a1=![]() ,a2=0(舍),
,a2=0(舍),
当a=![]() 时,AD=3a=2,
时,AD=3a=2,
∴AD=2;
(3)PF=FD,
理由是:∵∠APD=∠ABE=90°,∠PAD=∠BAE,
∴△APF∽△ABE,
∴![]() ,
,
∴PF=![]() ,
,
∵OE∥AD,
∴∠BOE=∠PAD,
∵∠OBE=∠APD=90°,
∴△ADP∽△OEB,
∴![]() ,
,
∴PD=![]() ,
,
∵AB=2OB,
∴PD=2PF,
∴PF=FD.