题目内容
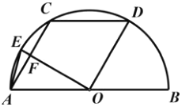
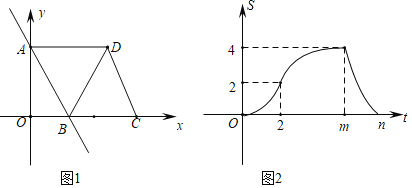
【题目】如图1，直线AB与x、y轴分别相交于点B、A，点C为x轴上一点，以AB、BC为边作平行四边形ABCD，连接BD，BD＝BC，将△AOB沿x轴从左向右以每秒一个单位的速度运动，当点O和点C重合时运动停止，设△AOB与△BCD重合部分的面积为S，运动时间为t秒，S与t之间的函数如图（2）所示（其中0＜t≤2，2＜t≤m，m＜t＜n时函数解析式不同）．
（1）点B的坐标为 ，点D的坐标为 ；
（2）求S与t的函数解析式，并写出t的取值范围．
【答案】（1）
（2）当0＜t≤2时，S＝
，当2＜t≤5时，S＝
，当5＜t＜7时，S＝t2﹣14t+49．
【解析】
（1）由图象可得当t＝2时，点O与点B重合，当t＝m时，△AOB在△BDC内部，可求点B坐标，过点D作DH⊥BC，可证四边形AOHD是矩形，可得AO＝DH，AD＝OH，由勾股定理可求BD的长，即可得点D坐标；
（2）分三种情况讨论，由相似三角形的性质可求解．
解：（1）由图象可得当t＝2时，点O与点B重合，
∴OB＝1×2＝2，
∴点B（2，0），
如图1，过点D作DH⊥BC，
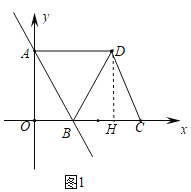
由图象可得当t＝m时，△AOB在△BDC内部，
∴4＝
×2×DH，
∴DH＝4，
∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，且DH⊥BC，
∴∠ADH＝∠DHO＝90°，且∠AOB＝90°，
∴四边形AOHD是矩形，
∴AO＝DH，AD＝OH，且AD＝BC＝BD，
∴OH＝BD，
∵DB2＝DH2+BH2，
∴DB2＝（DB﹣2）2+16，
∴DB＝5，
∴AD＝BC＝OH＝5，
∴点D（5，4），
故答案为：（2，0），（5，4）；
（2）∵OH＝BD＝BC＝5，OB＝2，
∴m＝
，n＝
＝7，
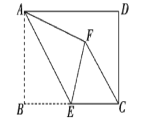
当0＜t≤2时，如图2，
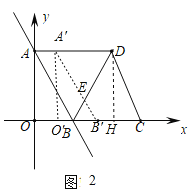
∵S△BCD＝BC×DH，
∴S△BCD＝10
∵A'B'∥CD，
∴△BB'E∽△BCD，
∴
＝（
）＝
，
∴S＝10×＝
t2，
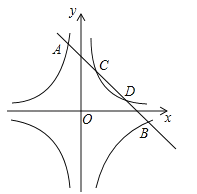
当2＜t≤5，如图3，
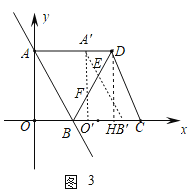
∵OO'＝t，
∴BO'＝t﹣2，FO'＝
（t﹣2），
∵S＝S△BB'E﹣S△BO'F＝t2﹣×（t﹣2）2，
∴S＝﹣
t2+
t﹣；
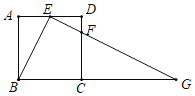
当5＜t＜7时，如图4，
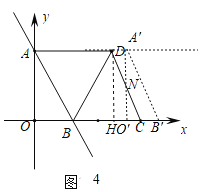
∵OO'＝t，
∴O'C＝7﹣t，O'N＝2（7﹣t），
∵S＝×O'C×O'N＝×2（7﹣t）2，
∴S＝t2﹣14t+49．
