题目内容
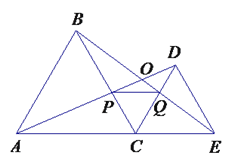
【题目】如图,A,B是两棵大树,两棵大树之间有一个废弃的圆形坑塘,为开发利用这个坑塘,需要测量A,B之间的距离,但坑塘附近地形复杂不容易直接测量.
(1)请你利用所学知识,设计一个测量A,B之间的距离的方案,并说明理由;
(2)在你设计的测量方案中,需要测量哪些数据?为什么?

【答案】(1)方案见解析,理由见解析;(2)见解析.
【解析】
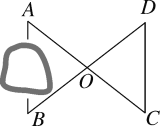
(1)①如图,过点B作射线BD,在射线BD上选取O、D两点,使OD=OB;②连接OA,并延长OA至点C,使OC=OA;③连接CD,则CD的长即为AB的长.根据SAS证明△AOB≌△COD,由全等三角形的性质即可得AB=CD.(2)由(1)可知,这个方案需要测量5个数据,即:线段OA,OB,OC,OD,CD的长度,并使OC=OA,OD=OB,则CD=AB.
(1)方案为:①如图,过点B画一条射线BD,在射线BD上选取O、D两点,使OD=OB;
②连接OA,并延长OA至点C,使OC=OA;
③连接CD,则CD的长即为AB的长.
理由如下:在△AOB和△COD中,
∵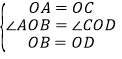 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
(2)根据这个方案,需要测量5个数据,即:线段OA,OB,OC,OD,CD的长度,并使OC=OA,OD=OB,则CD=AB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目