题目内容
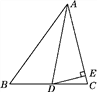
【题目】如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

【答案】(1)求证:①详见解析;②详见解析;(2)OE平分∠AED,理由详见解析.
【解析】
(1)①根据SAS即可判定.②由△OAC≌OBD,推出∠OAE=∠OBD,由△OAB是等边三角形,推出∠OAB+∠OBA=120°,推出∠OAE+∠BAE+∠OBA=120°,即∠EAB+∠EBA=120°,推出∠AEB=60°.
(2)OE平分∠AED.作OM⊥AC于M,ON⊥BD于N.由△OAC≌△OBD,推出S△OAC=S△OBD,推出![]() ACOM=
ACOM=![]() BDON,推出OM=ON,再根据角平分线判定定理即可证明.
BDON,推出OM=ON,再根据角平分线判定定理即可证明.
(1)证明:①∵△OAB与△OCD都是等边三角形,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.
②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2)解:OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
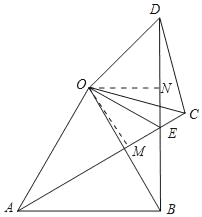
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴![]() ACOM=
ACOM=![]() BDON,
BDON,
∴OM=ON,
∴OE平分∠AED.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目