题目内容
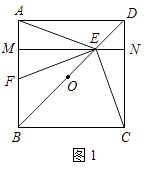
【题目】如图1，在平面直角坐标系中，直线l与x轴、y轴分别交于点B（4，0）、C（0，3），点A为x轴负半轴上一点，AM⊥BC于点M交y轴于点N（0， 
）．已知抛物线y=ax2+bx+c经过点A，B，C．
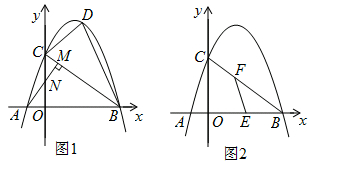
（1）求抛物线的函数式．
（2）连接AC，点D在线段BC上方的抛物线上，连接DC，DB，若△BCD和△ABC面积满足S△BCD= 
S△ABC ， 求点D的坐标．
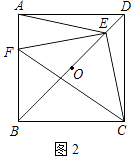
（3）如图2，E为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒3个单位的速度运动到F，再沿着线段PC以每秒5个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请直接写出最少时间和此时点F的坐标．
【答案】
（1）解：∵C（0，3），
∴OC=3，
∵4CN=5ON，
∴ON= 
，
∵∠OAN=∠NCM，
∴△AON∽△COB，
∴ 
= 
，即 
= 
，解得OA=1，
∴A（﹣1，0），
设抛物线解析式为y=a（x+1）（x﹣4），
把C（0，3）代入得a1（﹣4）=3，解得a=﹣ 
，
∴抛物线解析式为y=﹣ （x+1）（x﹣4）=﹣ x2+ 
x+3
（2）解：设直线BC的解析式为y=mx+n，
把C（0，3），B（4，0）代入得 
，解得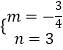 
，
∴直线BC的解析式为y=﹣ x+3，
作PQ∥y轴交BC于Q，如图1，设P（x，﹣ x2+ x+3），则Q（x，﹣ x+3），
DQ=﹣ x2+ x+3﹣（﹣ x+3）=﹣ x2+3x，
∴S△BCD=S△CDQ+S△BDQ= 
4（﹣ x2+3x）=﹣ 
x2+6x，
∵S△BCD= 
S△ABC，
∴﹣ x2+6x= × ×（4+1）×3，
整理得x2﹣4x+3=0，解得x1=1，x2=3，
∴D点坐标为（1， 
）或（3，3）；
（3）解：设F（x，﹣ x+3），则EF= 
= 
，CF= 
= 
x，
点P在整个运动过程中所用时间t= 
EF+ 
，
∴ EF+ ≥2 
，当EF= CF时，取等号，此时t最小，
即 
x2﹣ 
x+13=（ x）2得x1=2，x2= 
（舍去），
∴点P在整个运动过程中所用的最少时间2× ×2=3秒，此时点F的坐标为（2， ）．
【解析】（1）先证△AON∽△COB，利用相似三角形的性质可求得OA的长，可得A的坐标，从而设抛物线解析式为y=a（x+1）（x﹣4），再把C的坐标代入求出a的值，可得答案；
（2）利用待定系数法求出直线BC的解析式，作PQ∥y轴交BC于Q，设P
，则Q
，可表示出DQ，再由S△BCD=S△CDQ+S△BDQ和
得到x的方程，解此方程求出x的值，即可得D的坐标；
（3）设E
，表示出EF、CF的长，再由题意得t=EF+，又
，因为当EF=CF时，取等号，此时t最小，进而可得到关于x的方程，解方程求出符合条件的x值，进而可得F的坐标.
