题目内容
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知
，则球的半径长是（ ）
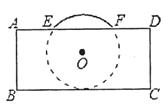
A. 2B. 2.5C. 3D. 4
【答案】B
【解析】
取EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，设OF=x，则OM=4-x，MF=2，然后在Rt△MOF中利用勾股定理求得OF的长即可．
如图：
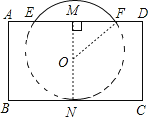
EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，
∵四边形ABCD是矩形，
∴∠C=∠D=90°，
∴四边形CDMN是矩形，
∴MN=CD=4，
设OF=x，则ON=OF，
∴OM=MN-ON=4-x，MF=2，
在直角三角形OMF中，OM2+MF2=OF2，
即：（4-x）2+22=x2，
解得：x=2.5，
故选：B．
练习册系列答案
相关题目
