题目内容
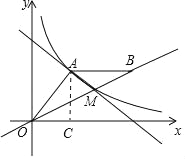
【题目】如图,A(8,6)是反比例函数y=![]() (x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=
(x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=![]() 的图象于点M
的图象于点M
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点M的坐标;
(3)设直线AM关系式为y=nx+b,观察图象,请直接写出不等式nx+b﹣![]() ≤0的解集.
≤0的解集.
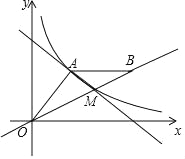
【答案】(1)y=![]() ;(2)M(12,4);(3)0<x≤8或x≥12.
;(2)M(12,4);(3)0<x≤8或x≥12.
【解析】
(1)根据待定系数法即可求得;
(2)利用勾股定理求得AB=OA=10,由AB∥x轴即可得点B的坐标,即可求得直线OB的解析式,然后联立方程求得点M的坐标;
(3)根据A、M点的坐标,结合图象即可求得.
解:(1)∵A(8,6)在反比例函数图象上
∴6=![]() ,即m=48,
,即m=48,
∴反比例函数y=的表达式为y=![]() ;
;
(2)∵A(8,6),作AC⊥x轴,由勾股定理得OA=10,
∵AB=OA,
∴AB=10,
∴B(18,6),
设直线OB的关系式为y=kx,
∴6=18k,
∴k=![]() ,
,
∴直线OB的关系式为y=![]() x,
x,
由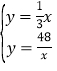 ,解得x=±12
,解得x=±12
又∵在第一象限
∴x=12
故M(12,4);
(3)∵A(8,6),M(12,4),
观察图象,不等式nx+b﹣![]() ≤0的解集为:0<x≤8或x≥12.
≤0的解集为:0<x≤8或x≥12.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目