题目内容
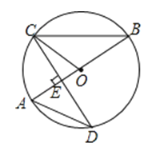
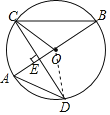
【题目】如图，
是圆
的直径．
是圆的一条弦．且
于点
．
(1)若
，求
的大小；
(2)若
．
，求弧
的长．
【答案】(1)
；(2)
．
【解析】
（1）首先求出∠ADE的度数，再根据圆周角定理求出∠AOC的度数，根据直角三角形的两个锐角互余求出∠OCE的度数；
（2）根据三角函数可求∠A=60°，可得∠BOD=120°，由弦CD与直径AB垂直，利用垂径定理得到E为CD的中点，求出DE、CE的长，在直角三角形OCE中，设圆的半径OC=r，OE=OA-AE，表示出OE，利用勾股定理列出关于r的方程，求出方程的解，即可得到圆的半径r的值，根据弧长的公式即可得到结论．
(1)∵
，
∴
∵
，
∴
．
∴
，
∴
；
(2)解：∵
是圆
的直径，且于点
，
∴
，
在
中，
，
∴
，
∴
，
在
中，
，
设圆的半径为
，则
，
，
所以
，
解得：
．∴圆的半径为4，
连接
，
∴弧
的长
．
练习册系列答案
相关题目
【题目】某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m分（60≤m≤100），组委会从1000篇征文中随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如图不完整的两幅统计图表．
征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
60≤m＜70 | 38 | 0.38 |
70≤m＜80 | a | 0.32 |
80≤m＜90 | b | c |
90≤m≤100 | 10 | 0.1 |
合计 | 1 |
请根据以上信息，解决下列问题：
（1）征文比赛成绩频数分布表中c的值是_____；
（2）补全征文比赛成绩频数分布直方图；
（3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．
