题目内容
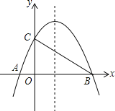
【题目】胖娃、猴子两人在1800米长的直线道路上跑步，胖娃、猴子两人同起点、同方向出发，并分别以不同的速度匀速前进.已知，胖娃出发30秒后，猴子出发，猴子到终点后立即返回，并以原来的速度前进，最后与胖娃相遇，此时跑步结束. 如图，
（米）表示胖娃、猴子两人之间的距离，x（秒）表示胖娃出发的时间，图中折线及数据表示整个跑步过程中y与x函数关系.那么，猴子到终点后_______秒与胖娃相遇.
【答案】
【解析】
根据速度＝路程÷时间可求出胖娃的速度，由猴子的速度＝胖娃的速度＋二者速度差可求出猴子的速度，利用时间＝路程÷速度可求出猴子到达终点的时间，结合路程＝速度×时间可求出此时胖娃离终点的距离，再根据相遇所需时间＝胖娃离终点的距离÷胖娃、猴子速度和，即可得出结论．
胖娃的速度为90÷30＝3（米/秒），
猴子的速度为3＋90÷（12030）＝4（米/秒）．
猴子到达终点时，胖娃出发的时间为1800÷4＋30＝480（秒），
此时胖娃离终点的距离为18003×480＝360（米），
猴子返回后与胖娃相遇的时间为360÷（3＋4）＝（秒）．
故答案为：．
练习册系列答案
相关题目
【题目】为弘扬泰山文化，我市某校举办了“泰山诗文大赛”活动，小学、初中部根据初赛成绩，各选出5名选手组成小学代表队和初中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩（满分为100分）如下图所示.
（1）根据图示填写图表；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
平均数（分） | 中位数（分） | 众数（分） | |
小学部 | 85 | ||
初中部 | 85 | 100 |
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
