Question

【题目】如图，在△ABC中，∠ABC＝45°，AD，BE分别为BC，AC边上的高，连接DE，过点D作DF⊥DE交BE于点F，G为BE中点，连接AF，DG．

（1）如图1，若点F与点G重合，求证：AF⊥DF；

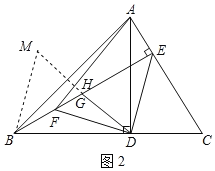
（2）如图2，请写出AF与DG之间的关系并证明．

Answer 1

【答案】（1）详见解析；（2）AF＝2DG，且AF⊥DG，理由详见解析．

【解析】

（1）设BE交AD于点H，证出△ABD是等腰直角三角形，得出AD=BD，证明△DAE≌△DBF（ASA），得出BF=AE，DF=DE，证出△FDE是等腰直角三角形，得出∠DFE=45°，再证明△AEF是等腰直角三角形，得出∠AFE=45°，即可得出结论；

（2）延长DG至M，使GM=DG，交AF于H，连接BM，证明△BGM≌△EGD（SAS），得出∠MBE=∠FED=45°=∠EFD，BM=DE=DF，由（1）知：∠DAC=∠DBE，再证明△BDM≌△DAF（SAS），得出DM=AF=2DG，∠FAD=∠BDM，证出∠AHD=90°，即可得出结论．

（1）设BE交AD于点H，如图1所示：

∵AD，BE分别为BC，AC边上的高，

∴∠BEA=∠ADB=90°．

∵∠ABC=45°，

∴△ABD是等腰直角三角形，

∴AD=BD．

∵∠AHE=∠BHD，

∴∠DAC=∠DBH．

∵∠ADB=∠FDE=90°，

∴∠ADE=∠BDF．

在△DAE和△DBF中，∵，

∴△DAE≌△DBF（ASA），

∴BF=AE，DF=DE，

∴△FDE是等腰直角三角形，

∴∠DFE=45°．

∵G为BE中点，

∴BF=EF，

∴AE=EF，

∴△AEF是等腰直角三角形，

∴∠AFE=45°，

∴∠AFD=90°，

∴AF⊥DF；

（2）AF=2DG，且AF⊥DG．理由如下：

延长DG至M，使GM=DG，交AF于H，连接BM，如图2所示：

在△BGM和△EGD中，∵，

∴△BGM≌△EGD（SAS），

∴∠MBE=∠FED=45°=∠EFD，BM=DE=DF，

由（1）知：∠DAC=∠DBE，

∴∠MBD=∠MBE+∠DBE=45°+∠DBE，∠EFD=45°=∠DBE+∠BDF，

∴∠BDF=45°﹣∠DBE．

∵∠ADE=∠BDF，

∴∠ADF=90°﹣∠BDF=45°+∠DBE=∠MBD．

在△BDM和△DAF中，∵，

∴△BDM≌△DAF（SAS），

∴DM=AF=2DG，∠FAD=∠BDM．

∵∠BDM+∠MDA=90°，

∴∠MDA+∠FAD=90°，

∴∠AHD=90°，

∴AF⊥DG，

∴AF=2DG，且AF⊥DG．