题目内容
【题目】如图,反比例函数![]() (k≠0)与一次函数y=ax+b(a≠0)相交于点A(1,3),B(c,﹣1).
(k≠0)与一次函数y=ax+b(a≠0)相交于点A(1,3),B(c,﹣1).
(1)求反比例函数与一次函数的解析式;
(2)在反比例函数图象上存在点C,使△AOC为等腰三角形,这样的点有几个,请直接写出一个以AC为底边的等腰三角形顶点C的坐标.

【答案】(1)反比例函数解析式为y=![]() ;一次函数解析式为y=x+2;(2)C点坐标为(﹣1,﹣3)或(3,1)或(﹣3,﹣1).
;一次函数解析式为y=x+2;(2)C点坐标为(﹣1,﹣3)或(3,1)或(﹣3,﹣1).
【解析】
(1)把点A(1,3)代入反比例函数的解析式即可求得k值,从而得到反比例函数的解析式;再把B(c,﹣1)代入反比例函数的解析式,求得c值,用待定系数法求一次函数的解析式即可;(2)分①以OA为腰时, AC为底、②以OA为腰时, OC为底、③以OA为底三种情况求点C的坐标即可.
(Ⅰ)∵点A(1,3)在反比例函数图象上,
∴k=1×3=3,
∴反比例函数解析式为y=![]() ;
;
∵B(c,﹣1)在反比例函数图象上,
∴c=﹣3,
∴B(﹣3,﹣1),
∵A、B在一次函数图象上,
∴![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=x+2;
(Ⅱ)当OA为腰时,若AC为底,则以O为圆心,OA为半径画圆,如图1,
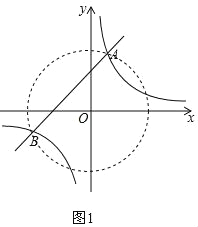
此时圆与反比例函数图象有3个交点,即满足条件的点C有三个;
若OC为底,则以A为圆心,OA长为半径画圆,如图2,
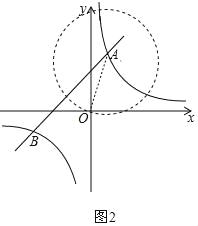
此时圆与反比例函数图象有两个交点,即满足条件的点C有两个;
当OA为底时,则点C在线段OA的垂直平分线上,如图3,
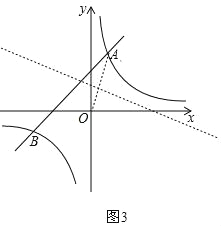
此时没有满足条件的点C;
综上可知满足条件的点C有5个;
可设C点坐标为(t,![]() ),
),
∵A(1,3),
∴OA2=12+32=10,OC2=t2+(![]() )2=t2+
)2=t2+![]() ,
,
当△AOC是以AC为底的等腰三角形时,则有OA=OC,即OA2=OC2,
∴10=t2+![]() ,解得t=1或t=﹣1或t=3或t=﹣3,
,解得t=1或t=﹣1或t=3或t=﹣3,
当t=1时,C与A重合,舍去,
∴C点坐标为(﹣1,﹣3)或(3,1)或(﹣3,﹣1).