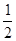题目内容
如图,矩形ABCD的边AB="6" cm,BC="8" cm,在BC上取一点P,在CD边上取一点Q,使∠APQ成直角,设BP="x" cm,CQ="y" cm,试以x为自变量,写出y与x的函数关系式.并求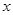 为何值时,
为何值时,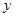 有最大值或最小值?
有最大值或最小值?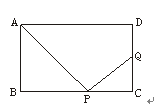
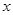 为何值时,
为何值时,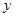 有最大值或最小值?
有最大值或最小值?
解:∵∠APQ=90°,
∴∠APB+∠QPC=90°。
∵∠APB+∠BAP=90°,
∴∠QPC=∠BAP,∠B=∠C=90°。
∴△ABP∽△PCQ。
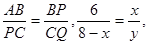
∴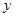 =-
=-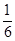
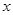 2+
2+
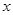 .
.
当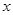 =4时,
=4时,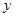 有最大值
有最大值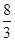
∴∠APB+∠QPC=90°。
∵∠APB+∠BAP=90°,
∴∠QPC=∠BAP,∠B=∠C=90°。
∴△ABP∽△PCQ。
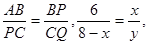
∴
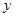 =-
=-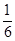
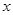 2+
2+
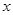 .
.当
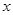 =4时,
=4时,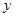 有最大值
有最大值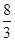
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
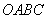 沿
沿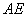 折叠,使点
折叠,使点 恰好落在
恰好落在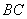 上
上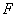 处,以
处,以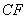 为边作正方形
为边作正方形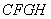 ,延长
,延长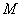 ,使
,使 ,再以
,再以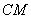 、
、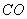 为边作矩形
为边作矩形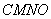 .
.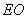 、
、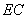 的大小,并说明理由.
的大小,并说明理由.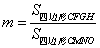 ,请问
,请问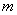 是否为定值?若是,请求出
是否为定值?若是,请求出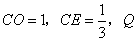 为
为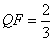 ,抛物线
,抛物线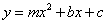 经过
经过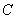 、
、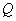 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.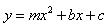 与线段
与线段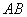 交于点
交于点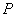 ,试问在直线
,试问在直线 ,使得以
,使得以 、
、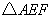 相似?若存在,请求直线
相似?若存在,请求直线 与
与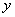 轴的交点
轴的交点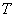 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
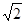 ︰1
︰1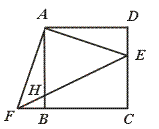
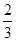 ,那么,你能求
,那么,你能求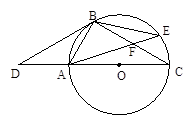 出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由. 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).
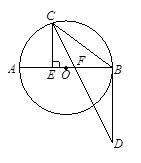
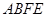 与正方形
与正方形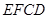 的位置如图所示.
的位置如图所示.
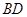 交
交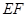 于点
于点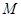 ;
;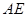 上取一点
上取一点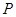 ,联结
,联结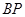 ,
,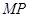 ,使△
,使△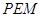 与△
与△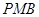 相似;
相似;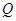 是线段
是线段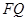 并延长交四边形
并延长交四边形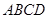 的一边于点
的一边于点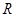 ,且满足
,且满足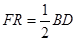 ,则
,则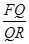 的值为______ _______.
的值为______ _______.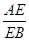 =
=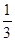 ,则
,则 的值为 【 】
的值为 【 】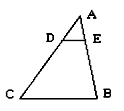
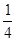 C、
C、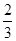 D、
D、