Question

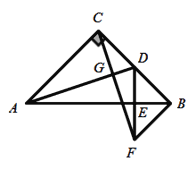
【题目】如图，在四边形ABCD中，AB=CD，BD是对角线．分别过点A、C作AE⊥BD于点E，CF⊥BD于点F，且AE=CF

（1）求证：AB∥CD

（2）若E是BF中点，且△ABE的面积为1，则四边形ABCD的面积为________.

Answer 1

【答案】(1)详见解析;(2)6

【解析】

（1）由AE⊥BD，CF⊥BD，根据垂直的定义得到∠AEB=∠DFC，和已知AE=CF，BF=DE，推出△ABE≌△CDF，进而∠ABE=∠CDF，由内错角相等两直线平行即可得证；

（2）由（1）可知∠ABE=∠CDF，再结合AB=CD，BD=DB可证△ABD≌Rt△CDB，由Rt△ABE≌Rt△DCF可得BE=DF，结合E是BF中点即BE=EF，得S△ABD=3S△ABE，从而S四边形ABCD=2S△ABD=6.

（1）证明：∵AE⊥BD，CF⊥BD，

∴∠AEB=∠CFD=90°

∵AB=CD， AE=CF，

∴Rt△ABE≌Rt△DCF

∴∠ABE=∠CDF

∴AB∥CD

（2）由（1）可知∠ABE=∠CDF，

∵AB=CD，BD=DB，

∴△ABD≌△CDB，

∴S△ABD=3S△CDB，

∵Rt△ABE≌Rt△DCF，

∴BE=DF，

∵E是BF中点，

∴BE=EF，

∴S△ABD=3S△ABE=3，

∴S四边形ABCD=2S△ABD=6.

故答案为：6