��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���A����4��0����B��0����4����C��2��0�����㣮
��1���������߽���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����MOA�����ΪS����S����m�ĺ�����ϵʽ���������mΪ��ֵʱ��S�����ֵ��������ֵ�Ƕ��٣�
��3������Q��ֱ��y=��x�ϵĶ��㣬��Q��y���ƽ���߽��������ڵ�P���ж��м���Q��ʹ�Ե�P��Q��B��OΪ������ı�����ƽ���ı��εĵ㣬ֱ��д����Ӧ�ĵ�Q�����꣮

���𰸡���1��y=![]() x2+x��4����2��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9����3��Q����Ϊ����4��4����2+2
x2+x��4����2��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9����3��Q����Ϊ����4��4����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��������
(1)�������߽���ʽΪy�� ax2 �� bx �� c,Ȼ��ѵ�A��B��C��������뺯������ʽ�����ô���ϵ������⼴��;
(2)���������ߵĽ���ʽ��ʾ����M�������꣬�Ӷ��õ���M��x��ľ��룬Ȼ����������������ʽ��ʾ���������ɵý⣬���������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý�;
(3)����ֱ���������ߵĽ���ʽ��ʾ����P��Q�����꣬Ȼ�����PQ�ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������x��һԪ���η��̼��ɵý�.
�⣺��1���������߽���ʽΪy=ax2+bx+c��
�������߾���A����4��0����B��0����4����C��2��0����
��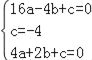 ��
��
���![]() ��
��
�������߽���ʽΪy=![]() x2+x��4��
x2+x��4��
��2������M�ĺ�����Ϊm��
����M��������Ϊ![]() m2+m��4��
m2+m��4��
����A����4��0����
��AO=0������4��=4��
��S=![]() ��4��|
��4��|![]() m2+m��4|=����m2+2m��8��=��m2��2m+8��
m2+m��4|=����m2+2m��8��=��m2��2m+8��
��S=����m2+2m��8��=����m+1��2+9����MΪ������������������һ���㣬
����m=��1ʱ��S�����ֵ�����ֵΪS=9��
�ʴ�Ϊ��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9��
��3������Q��ֱ��y=��x�ϵĶ��㣬
�����Q��������a����a����
����P���������ϣ���PQ��y�ᣬ
����P��������a��![]() a2+a��4����
a2+a��4����
��PQ=��a����![]() a2+a��4��=��
a2+a��4��=��![]() a2��2a+4��
a2��2a+4��
����OB=0������4��=4��
�Ե�P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��|PQ|=OB��
��|��![]() a2��2a+4|=4��
a2��2a+4|=4��
�٩�![]() a2��2a+4=4ʱ�������ã�a2+4a=0��
a2��2a+4=4ʱ�������ã�a2+4a=0��
���a=0����ȥ����a=��4��
��a=4��
���Ե�Q����Ϊ����4��4����
�ک�![]() a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
���a=��2��2![]() ��
��
���Ե�Q������Ϊ����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ����
����
����������Q��������4��4����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�

 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�


