��Ŀ����
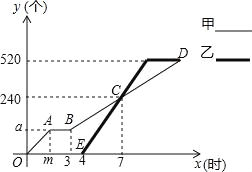
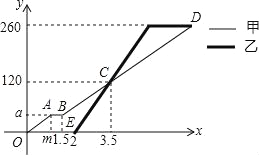
����Ŀ���ס�����̨�������Լӹ���ͬ���������������ʱ����Ч�ʲ��䣬�����ȿ�ʼ��������;ͣ��������0.5Сʱ����ͼ�Ǽס�����̨�������������������и��Լӹ����������y���������������ʱ��x��ʱ��֮��ĺ���ͼ��
��1����ͼ��m��a��ֵ��
��2������������ӹ����������y��x֮��ĺ�����ϵʽ��
��3�����һ��������ڼ䣬����̨�����ӹ�������������50��ʱx��ֵ��
���𰸡�(1) m=1��a=40��(2) y=40x-20��3.5��x��7����(3) ����������![]() Сʱ��
Сʱ��![]() Сʱʱ��ǡ�����50����
Сʱʱ��ǡ�����50����
��������
�������: ��1��������֪��ͼ����Եõ�m��ֵ���ɼס�����̨�������Լӹ���ͬ���������������ʱ����Ч�ʲ��䣬�������a��ֵ��
��2����ͼ����Եõ���B��C�ĵ�����꣬�Ӷ����Եõ��������ӹ����������y��x֮��ĺ�����ϵʽ��
��3��������������г���Ӧ�ĵ�ʽ���Ӷ��������x��ֵ��
�����������1��������ɵã�
m=1.5-0.5=1��
�߹���Ч�ʱ��ֲ��䣬
��![]() �����a=40��
�����a=40��
��m=1��a=40��
��2����������ӹ����������y��x֮��ĺ�����ϵʽ�ǣ�y=k1x+b1��
��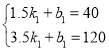 ��
��
��ã�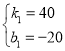
���������ӹ����������y��x֮��ĺ�����ϵʽ�ǣ�y=40x-20��3.5��x��7����
��3����CE����ֱ�ߵĺ�������ʽΪ��y=k2x+b2��
��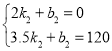
��ã�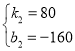 ��
��
��ֱ��CE����ֱ�ߵĽ���ʽΪ��y=80x-160��
��|��80x-160��-��40x-20��|=50��
��ã�x=![]() ��x=
��x=![]() ��
��
������������![]() Сʱ��
Сʱ��![]() Сʱʱ��ǡ�����50����
Сʱʱ��ǡ�����50����