题目内容
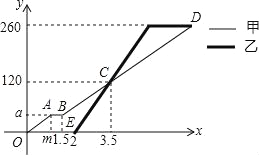
【题目】甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.
(1)图中m= ,a= .
(2)求重新工作后甲加工的零件个数y与x之间的函数关系式.
(3)求乙工作期间两人加工的零件个数相差100个时x的值.
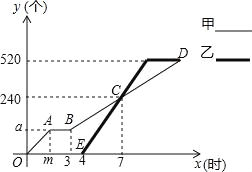
【答案】(1)2;80;(2)y=40x-40;(3)乙工作期间两人加工的零件个数相差100个时x的值是4.5小时或9.5小时.
【解析】
试题分析:(1)根据题意列方程即可得到结论;
(2)设y与x之间的函数关系式为y=kx+b,列方程组即可得到结论;
(3)设直线CE的函数关系式为y=kx+b,求得直线CE的函数关系式为y=80x-320,根根据题意列方程即可得到结论.
试题解析:(1)m=3-1=2,
根据题意得:![]() ,
,
解得:a=80.
(2)设y与x之间的函数关系式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴y与x之间的函数关系式为y=40x-40;
(3)设直线CE的函数关系式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴直线CE的函数关系式为y=80x-320,
根据题意得:(80x-320)-(40x-40)=100,
解得:x=![]() =4.5,或x=
=4.5,或x=![]() =9.5.
=9.5.
答:乙工作期间两人加工的零件个数相差100个时x的值是4.5小时或9.5小时.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目