��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�У���P��x��y���ĺ�����x�ľ���ֵ��ʾΪ|x|��������y�ľ���ֵ��ʾΪ|y|�����ǰѵ�P��x��y���ĺ�������������ľ���ֵ֮�ͽ�����P��x��y���Ĺ���ֵ����Ϊ��P��������P��=![]() +
+![]() �������еġ�+�������������еļӷ���
�������еġ�+�������������еļӷ���
��1�����A����1��3����B��![]() ��
��![]() ���Ĺ���ֵ��A������B����
���Ĺ���ֵ��A������B����
��2����M�ڷ���������![]() ��ͼ���ϣ��ҡ�M��=4�����M�����ꣻ
��ͼ���ϣ��ҡ�M��=4�����M�����ꣻ
��3��������������N��=3�����е�NΧ�ɵ�ͼ�ε������
���𰸡���1����A��=4����B��=4����2��M��1��3����M����1����3����M��3��1����M����3����1������3��18��
��������
�����������1���ɹ���ֵ�Ķ��弴����⣻
��2����M�ڷ���������![]() ��ͼ���ϣ��ҡ�M��=4���з����鼴�ɵõ������
��ͼ���ϣ��ҡ�M��=4���з����鼴�ɵõ������
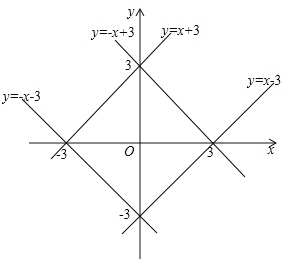
��3����N�������Ϊ��x��y�����ɡ�N��=3���õ�����|x|+|y|=3���õ�x+y=3����x��y=3��x��y=3����x+y=3����Ϊһ�κ����Ľ���ʽy=��x+3��y=��x��3��y=x��3��y=x+3�����ǵõ����е�NΧ�ɵ�ͼ���DZ߳�Ϊ![]() �������Σ����������
�����������������
�����������1����A����1��3����B��![]() ��
��![]() ��������A��=|��1|+|3|=4����B��=
��������A��=|��1|+|3|=4����B��=![]() =4��
=4��
��2���裺��M������Ϊ��m��n��������������������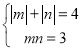 ����ã�
����ã�![]() ��
��![]() ��
��![]() ��
��![]() ����M��1��3��������1����3������3��1��������3����1����
����M��1��3��������1����3������3��1��������3����1����
��3����N�������Ϊ��x��y��������N��=3����|x|+|y|=3����x+y=3����x��y=3��x��y=3����x+y=3����y=��x+3��y=��x��3��y=x��3��y=x+3����ͼ�����е�NΧ�ɵ�ͼ�ε����=![]() =18��
=18��