题目内容
如图,已知点A(1,m)和点B(3,n)是一次函数 图象与反比例函数
图象与反比例函数 图象的交点.过点A作AM⊥x轴,垂足为 M,连结BM. 若AM= BM.
图象的交点.过点A作AM⊥x轴,垂足为 M,连结BM. 若AM= BM.

(1)求点B的坐标和一次函数的解析式;
(2)求△AMB的面积.
 图象与反比例函数
图象与反比例函数 图象的交点.过点A作AM⊥x轴,垂足为 M,连结BM. 若AM= BM.
图象的交点.过点A作AM⊥x轴,垂足为 M,连结BM. 若AM= BM.
(1)求点B的坐标和一次函数的解析式;
(2)求△AMB的面积.
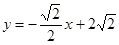 ;
;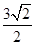
试题分析:解:∵点A(1,m和点B (3,n )在反比例函数y=
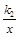 (k2>0)图象上,
(k2>0)图象上,∴ m=k2=3n .
∴ AM=3n.
过点B作BT⊥AM,垂足为T,如图1,∴ BT=2, TM=n.

∵ AM=BM, ∴ BM=3n.
在Rt△BTM中,TM 2+BT2=BM2,∴ n2+4=9n2,∴n=
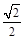 ,
,∴点B(3,
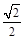 ). 4分
). 4分A(1,
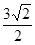 ) .
) . 将B(3,
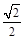 ),A(1,
),A(1,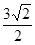 )代入
)代入
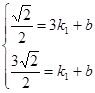 ,解之得
,解之得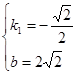
所以一次函数的解析式为:
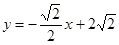 8分
8分(2)
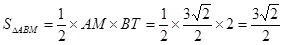
点评:解答本题的关键是要分析题意根据实际意义准确的求出解析式,并会根据图示得出所需要的信息.同时注意要根据实际意义准确的找到不等关系,利用不等式组求解.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 (件)与时间
(件)与时间 (时)的函数图象如图所示.
(时)的函数图象如图所示.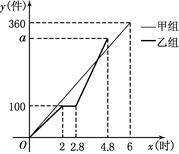
 的值.
的值. 
 、
、 两地,现用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往
两地,现用大、小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆,运往 与
与 轴,
轴, 轴分别相交于点
轴分别相交于点 .点
.点 从点
从点 出发沿射线
出发沿射线 以每秒1个单位长的速度匀速运动,同时点
以每秒1个单位长的速度匀速运动,同时点 从点
从点 出发沿
出发沿 以每秒1个单位长的速度向点
以每秒1个单位长的速度向点 匀速运动.当点
匀速运动.当点 ,
, 交
交 .记
.记 关于
关于 .设点
.设点 运动的时间是秒(
运动的时间是秒( ).
).
 时,则
时,则 = ,点
= ,点 时,若记四边形BDCO的面积为S,则求S关于的函数解析式
时,若记四边形BDCO的面积为S,则求S关于的函数解析式 为等腰直角三角形时,请直接写出的值
为等腰直角三角形时,请直接写出的值