题目内容
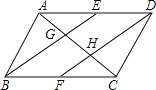
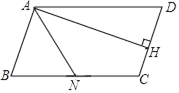
【题目】如图,ABCD中,AD=2AB,AH⊥CD于点H,N为BC中点,若∠D=68°,则∠NAH=_____.
【答案】34°
【解析】
由平行四边形的性质得出AD=BC,∠B=∠D=68°,∠BAD=180°﹣∠D=112°,证出AB=BN,由等腰三角形的性质得出∠BAN=∠ANB=56°,由直角三角形的性质得出∠DAH=90°﹣∠D=22°,即可求出∠NAH的度数.
解:∵四边形ABCD是平行四边形,
∴AD=BC,∠B=∠D=68°,∠BAD=180°﹣∠D=112°,
∵N为BC中点,
∴BC=2BN,
∵BC=AD=2AB,
∴AB=BN,
∴∠BAN=∠ANB=![]() (180°﹣68°)=56°,
(180°﹣68°)=56°,
∵AH⊥CD,
∴∠DAH=90°﹣∠D=22°,
∴∠NAH=∠BAD﹣∠BAN﹣∠DAH=34°;
故答案为:34°.

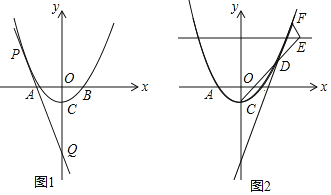
【题目】数学学习小组根据函数学习的经验,对一个新函数![]() 的图象和性质进行了如下探究:
的图象和性质进行了如下探究:
![]() 列表,下表是函数
列表,下表是函数![]() 与自变量
与自变量![]() 的几组对应值
的几组对应值
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
请直接写出![]()
![]()
![]()
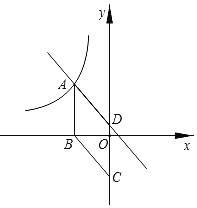
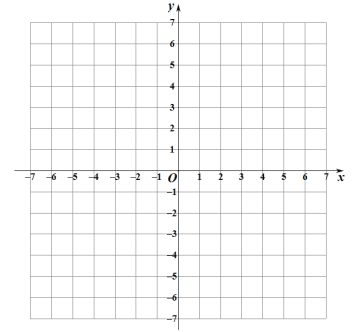
![]() 如图,在平面直角系
如图,在平面直角系![]() 中,描出上表中各对对应值为坐标的点 (其中
中,描出上表中各对对应值为坐标的点 (其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出函数的图象
为纵坐标),并根据描出的点画出函数的图象
![]() 观察所画出的函数图象,写出该函数的性质(写一条性质即可)
观察所画出的函数图象,写出该函数的性质(写一条性质即可)
![]() 请结合画出的函数图象与表格中数据,直接写出关于
请结合画出的函数图象与表格中数据,直接写出关于![]() 的不等式的解集:
的不等式的解集:![]()
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如下表:
的关系如下表:
时间 | 1 | 3 | 5 | 10 | 36 |
|
日销售量 | 94 | 90 | 86 | 76 | 24 |
|
已知未来40天内,前20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数),后20天该商品每天的价格
,且t为整数),后20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数).
,且t为整数).
![]() 求m与t之间的函数关系式;
求m与t之间的函数关系式;
![]() 未来40天内,后20天中哪一天的日销售利润最大
未来40天内,后20天中哪一天的日销售利润最大![]() 最大日销售利润是多少.
最大日销售利润是多少.
![]() 在实际销售的前20天中,该公司决定每销售一件商品,就捐赠
在实际销售的前20天中,该公司决定每销售一件商品,就捐赠![]() 元给希望工程
元给希望工程![]() 公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.