题目内容
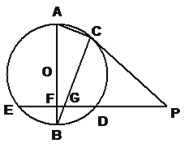
【题目】已知,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直于AB于点F,交BC于点G,∠A=∠BCP.
(1)求证:PC是⊙O的切线;
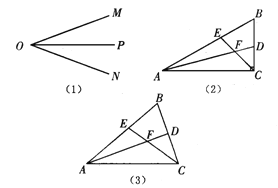
(2)若点C在劣弧AD上运动,其条件不变,问应再具备什么条件可使结论BG2=BF·BO成立,(要求画出示意图并说明理由).
【答案】见解析
【解析】试题分析:(1)证PC是⊙O的切线,即证∠OCP=90°,而∠OCP=∠BCP+∠OCB=∠A+∠OBC,因为AB为直径,直径所对的圆周角为直角,即可证明.
(2)BG2=BFBO要成立,Rt△BFG和Rt△BGO必须相似,而他们已经共用了一角B,所以如果相似,则必有∠BFG=∠BGO=90°,根据垂径定理,G点必在BC中点处.
试题解析:(1)证明:连接OC.∵OA=OC,∴∠A=∠OCA.∵AB为直径,∴∠OCA+∠OCB=90°,∴∠OCP=∠BCP+∠OCB=90°,即PC是⊙O的切线.
(2)解:添加条件为:G为BC的中点.
连接OG.∵G为BC的中点,∴OG⊥BC又FG⊥BO,∴Rt△BFG∽Rt△BGO,∴ ![]() ,即BG2=BFBO.
,即BG2=BFBO.


练习册系列答案
相关题目