题目内容
(本小题满分6分)在下面三小题中任选其中两小题完成

(1)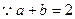
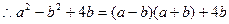
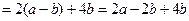
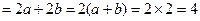
(2)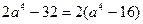
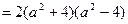

(3)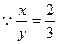 ,不妨设
,不妨设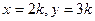
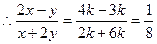 解析:
解析:
略
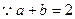
|
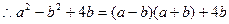
|
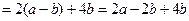
|
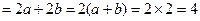
|
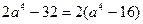
|
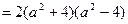
|

|
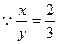 ,不妨设
,不妨设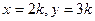
|
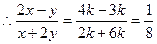 解析:
解析:略

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 (
(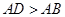 )中,将纸片折叠一次,使点
)中,将纸片折叠一次,使点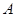 与
与 重合,再展开,折痕
重合,再展开,折痕 交
交 边于
边于 ,交
,交 边于
边于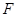 ,分别连结
,分别连结 和
和 .
.
 是菱形;
是菱形; 交
交 于
于 ,求证:
,求证:
 ,
, 的面积为
的面积为 ,求
,求
 为半径的圆的内部的概率.
为半径的圆的内部的概率. 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.