题目内容
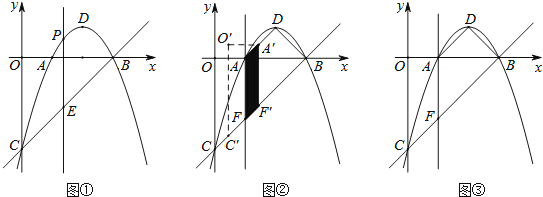
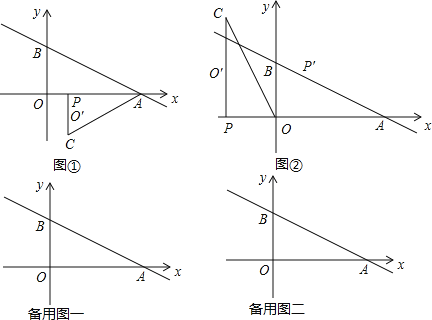
【题目】如图①,已知直线y=﹣![]() x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
x+3分别交x轴,y轴于点A,点B.点P是射线AO上的一个动点.把线段PO绕点P逆时针旋转90°得到的对应线段为PO′,再延长PO′到C使CO′=PO′,连结AC,设点P坐标为(m,0),△APC的面积为S.
(1)直接写出OA和OB的长,OA的长是 ,OB的长是 ;
(2)当点P在线段OA上(不含端点)时,求S关于m的函数表达式;
(3)当以A,P,C为顶点的三角形和△AOB相似时,求出所有满足条件的m的值;
(4)如图②,当点P关于OC的对称点P′落在直线AB上时,m的值是 .
【答案】(1)6,3;(2)S=![]() (6﹣m)2m=﹣m2+6m(0<m<6);(3)m=3,m=1.2,m=﹣2;(4)﹣
(6﹣m)2m=﹣m2+6m(0<m<6);(3)m=3,m=1.2,m=﹣2;(4)﹣![]() .
.
【解析】
试题分析:(1)根据自变量与函数值的对应关系,可得A、B点坐标,可得OA,OB的长;
(2)根据旋转的性质,可得PO′,根据线段中点的性质,可得PC的长,根据三角形的面积公式,可得答案;
(3)根据相似三角形的性质,可得关于m的方程,根据解方程,可得答案;
(4)根据待定系数法,可得OC的解析式,PP′的解析式,根据解方程组,可得D点坐标,根据中点的坐标公式,可得P′点坐标,根据图象上的点满足函数解析式,可得关于m的方程,根据解方程,可得答案.
解:(1)由直线y=﹣![]() x+3可知A(6,0),B(0,3),
x+3可知A(6,0),B(0,3),
∴OA=6,OB=3,
故答案为:6,3;
(2)∵点P坐标为(m,0),
∴OP=m.
∵线段PO绕点P逆时针旋转90°,得
对应线段为PO′=m.
再延长PO′到C使CO′=PO′,
∴PC=2m.
∵PA=6﹣m,
∴S=![]() (6﹣m)2m=﹣m2+6m(0<m<6);
(6﹣m)2m=﹣m2+6m(0<m<6);
(3)当0≤m<6时,
∵以A,P,C为顶点的三角形和△AOB相似,
∴![]() =
=![]() ,解得m=3,
,解得m=3,
或![]() =
=![]() ,解得m=1.2;
,解得m=1.2;
当m<0时,
∵以A,P,C为顶点的三角形和△AOB相似,
∴![]() =
=![]() ,m的值不存在,
,m的值不存在,
或![]() =
=![]() ,解得m=﹣2,
,解得m=﹣2,
综上所述:m=3,m=1.2,m=﹣2;
(4)如图1:
 ,
,
P(m,0),C(m,﹣2m)
OC的解析式为y=﹣2x,
PP′的解析式为y=![]() x﹣
x﹣![]() m,
m,
联立OC与PP′,得 ,
,
解得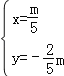 ,
,
D(![]() ,﹣
,﹣![]() m),
m),
P′横坐标2×![]() ﹣m=﹣
﹣m=﹣![]() m,纵坐标2×(﹣
m,纵坐标2×(﹣![]() m)﹣0=﹣
m)﹣0=﹣![]() m,
m,
P′(﹣![]() m,﹣
m,﹣![]() m).
m).
将P′点的坐标代入AB,得
﹣![]() m=﹣
m=﹣![]() ×(﹣
×(﹣![]() m)+3,
m)+3,
解得m=﹣![]() ,
,
故答案为:﹣![]() .
.

【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
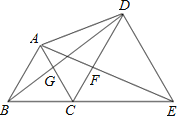
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA