��Ŀ����
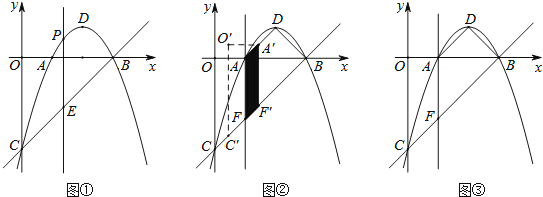
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C����BAC��ƽ������y�ύ�ڵ�D�����������ཻ�ڵ�Q��P���߶�AB��һ�㣬����P��x��Ĵ��ߣ��ֱ�AD��AC�ڵ�E��F������BE��BF��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C����BAC��ƽ������y�ύ�ڵ�D�����������ཻ�ڵ�Q��P���߶�AB��һ�㣬����P��x��Ĵ��ߣ��ֱ�AD��AC�ڵ�E��F������BE��BF��
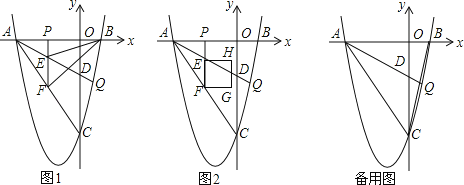
��1����ͼ1�����߶�AC����ֱ�ߵĽ���ʽ��
��2����ͼ1������BEF��������ֵ�ʹ�ʱ��P�����ꣻ
��3����ͼ2����EFΪ�ߣ��������Ҳ���������EFGH����P���߶�AB���˶�ʱ������EFGHҲ��֮�˶��ͱ仯����������EFGH�Ķ���G��H���߶�BC��ʱ����������EFGH�ı߳���
���𰸡���1��![]() ����2����x=��1ʱ��S��BEF�����ֵ=
����2����x=��1ʱ��S��BEF�����ֵ=![]() ��P����1��0������3������G���߶�BC��ʱ��
��P����1��0������3������G���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ������H���߶�BC��ʱ��
������H���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ��
��
��������
�����������1���������߽���ʽ��õ�A��C�����꣬Ȼ����ݴ���ϵ��������ֱ��AC��ֱ�߷��̼��ɣ�
��2�����ͼ2����ֱ��������AOC�����ù��ɶ������AC�ij��ȣ�����D��DI��AC�ڵ�I������ȫ����������ADI�ա�ADO��SSA����Rt��CDI������ȫ�������ε����ʿ�����DI=DO=m����DC=OC��OD=4��m�����Ը��ݹ��ɶ����г�����m�ķ��̣������ڷ��̽��⼴����õ�D�����ꣻȻ�����ô���ϵ�������ֱ��AD���̣���ֱ���ϵ�����������������ε������ʽ�Ͷ��κ�����ֵ����������BEF��������ֵ�ʹ�ʱ��P�����ꣻ
��3����Ҫ�������ۣ��ٵ�����G���߶�BC��ʱ�����ͼ3����P��t��0��������һ�κ���ͼ���ϵ�����������������ε�������֪![]() ��
��![]() ��
��![]() �������������ε��ڱ���ȵõ���
�������������ε��ڱ���ȵõ���![]() ����EF��FG�ij��ȣ��Ӷ���õ�P������������εı߳���
����EF��FG�ij��ȣ��Ӷ���õ�P������������εı߳���
ͬ�����ڵ�����H���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ��
��
�⣺��1�����ͼ1�������ߵĽ���ʽΪ��![]() ��
��

��x=0����y=��4��
��C��0����4����
��y=0����![]() ��
��
��ã�x1=��3��x2=1��
��A����3��0����B��1��0����
��ֱ��AC����ֱ�߽���ʽΪ��y=kx+b��k��0����
��A����3��0����C��0����4������ɵã�![]() ��
��
��� ��
��
ֱ��AC����ֱ�߽���ʽΪ��![]() ��
��
��2������D��DI��AC�ڵ�I�����ͼ2��

��A����3��0����C��0����4����
��OA=3��
��OC=4��
��Rt��AOC��![]() ��
��
������ADI����ADO�� ��
��
���ADI�ա�ADO��SSA����
��AI=AO=3��DI=DO��
��DI=DO=m����DC=OC��OD=4��m��
��IC=AC��AI��
��IC=5��3=2��
��Rt��CDI����ID2+IC2=DC2��
��m2+22=��4��m��2��
��ã�![]() ��
��
��![]() ��
��
��![]() ��
��
��ֱ��AD����ֱ�߽���ʽΪ��y=kx+b��k��0����
��A����3��0����![]() ����ɵã�
����ɵã� ��
��
��� ��
��
ֱ��AD����ֱ�߽���ʽΪ��![]() ��
��
����ֱ��AC�Ľ���ʽΪ��![]() ��
��
����P��n��0������![]() ��
��![]() ��
��
��BP=1��n��![]() ��
��
��![]() =
=![]() ��
��
���ú����ĶԳ�����ֱ��x=��1��
����x=��1ʱ��S��BEF�����ֵ=![]() ��
��
��ʱ��P����1��0����
��3����B��1��0����C��0����4���ɵ�ֱ��BC�Ľ���ʽΪ��y=4x��4��
�ٵ�����G���߶�BC��ʱ�����ͼ3��

��P��t��0������![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��EF=FG��
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��
������G���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ��
��
�ڵ�����H���߶�BC��ʱ�����ͼ4��

��P��t��0������![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��EF=EH��
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��
������H���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ��
��
��������������G���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ������H���߶�BC��ʱ��
������H���߶�BC��ʱ��![]() �������εı߳�Ϊ
�������εı߳�Ϊ![]() ��
��

����Ŀ�����κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
x | �� | 0 | 1 | 2 | �� |
y | �� | 4 | ��4 | 6 | �� |
��1��ac��0����2����x��1ʱ��y��ֵ��xֵ�����������3����1�Ƿ���ax2+bx+c=0��һ��������4������1��x��2ʱ��ax2+bx+c��0��������ȷ�ĸ���Ϊ�� ��
A��4�� B��3�� C��2�� D��1��