题目内容
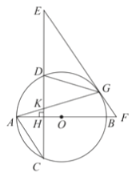
【题目】如图,在 Rt△ABC 中,∠ABC=90°,AB=BC,点 D 是线段 AB 上的一点,连结 CD.过点 B 作 BG⊥CD,分别交 CD、CA 于点 E、F,与过点 A 且垂直于 AB 的直线相交于点 G,连结 DF,给出以下四个结论:①![]() ;②若
;②若![]()
![]() AB,则点 D 是 AB 的中点;③若
AB,则点 D 是 AB 的中点;③若![]() ,则 S△ABC=9S△BDF;④当 B、C、F、D 四点在同一个圆上时,DF=DB;其中正确的结论序号是( )
,则 S△ABC=9S△BDF;④当 B、C、F、D 四点在同一个圆上时,DF=DB;其中正确的结论序号是( )

A.①②B.①②④C.①②③D.①②③④
【答案】B
【解析】
由![]() 可得:
可得:![]() ,所以
,所以![]() ,利用相似三角形的性质可以得到①正确;由
,利用相似三角形的性质可以得到①正确;由![]() 以及已知条件可以得到
以及已知条件可以得到![]() ,进而由①所得结论确定
,进而由①所得结论确定![]() 为
为![]() 的三等分点,可确定结论②正确;根据
的三等分点,可确定结论②正确;根据![]() 可以得到
可以得到![]() ,
,![]() ,则
,则![]() ,由线段的比例关系即可求得面积的比例关系;当
,由线段的比例关系即可求得面积的比例关系;当![]() 四点在同一个圆上时,利用圆内接四边形的对角互补可以得到
四点在同一个圆上时,利用圆内接四边形的对角互补可以得到![]() ,则
,则![]() 是
是![]() 所在圆的直径,由垂径定理可得
所在圆的直径,由垂径定理可得![]() ;
;
由题意可得:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故结论①正确;
![]()
![]()
![]() ,
,![]()
![]() ,
,![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]() 在
在![]() 和
和![]() 中:
中: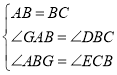
![]()
![]()
![]()
![]()
![]() 是等腰直角三角形,
是等腰直角三角形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
由结论①可得:![]()
![]()
![]()
![]() 点
点![]() 是
是![]() 的中点
的中点
故结论②正确;
![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,即
,即![]()
故结论③错误;
当![]() 四点在同一个圆上时,
四点在同一个圆上时,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 是
是![]() 所在圆的直径
所在圆的直径
![]()
![]()
![]()
![]()
![]()
故结论④正确;
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目