题目内容
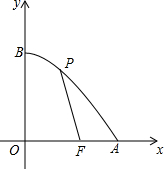 (2012•黄冈模拟)如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
(2012•黄冈模拟)如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-| 3 |
| 5 |
y2=-
x2+16
| 16 |
| 25 |
y2=-
x2+16
.| 16 |
| 25 |
分析:过点P作PC⊥x轴于点C,根据勾股定理得PF2=PC2+FC2,建立关于x、y的函数关系式,从而得到关于x的二次函数.
解答: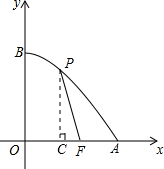 解:过点P作PC⊥x轴于点C,
解:过点P作PC⊥x轴于点C,
则由勾股定理得:
PF2=PC2+FC2,
则d2=(3-x)2+y2,
∵d=5-
x,
∴(5-
x)2=(3-x)2+y2.
整理得,y2=-
x2+16.
故答案为y2=-
x2+16.
 解:过点P作PC⊥x轴于点C,
解:过点P作PC⊥x轴于点C,则由勾股定理得:
PF2=PC2+FC2,
则d2=(3-x)2+y2,
∵d=5-
| 3 |
| 5 |
∴(5-
| 3 |
| 5 |
整理得,y2=-
| 16 |
| 25 |
故答案为y2=-
| 16 |
| 25 |
点评:本题考查了待定系数法求二次函数解析式、勾股定理,巧用P的坐标是解题的关键.

练习册系列答案
相关题目
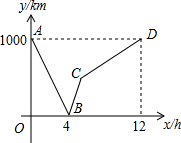 (2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )
(2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )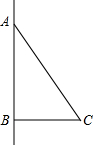 (2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是
(2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是