题目内容
(2012•黄冈模拟)某校九年级全体500名女生进行仰卧起坐训练,下图是随机抽取的若干名女生训练前“1分钟仰卧起坐”测试的成绩统计图.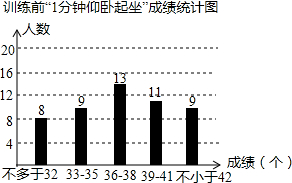
(1)若将训练前女生的成绩用扇形图来表示,则第三成绩段(从左到右)的圆心角为
(2)若将(1)中女生训练后的成绩用条形图来表示,前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,求其余各成绩段的人数?
(3)若规定39个以上(含39个)为优秀等级,请根据两次测试成绩,估算该校九年级全体女生优秀等级人数训练后比训练前增加了多少人?

(1)若将训练前女生的成绩用扇形图来表示,则第三成绩段(从左到右)的圆心角为
93.6
93.6
度.(2)若将(1)中女生训练后的成绩用条形图来表示,前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,求其余各成绩段的人数?
(3)若规定39个以上(含39个)为优秀等级,请根据两次测试成绩,估算该校九年级全体女生优秀等级人数训练后比训练前增加了多少人?
分析:(1)根据上图中的左图可知,随机抽取女生训练前后“1分钟仰卧起坐”的总人数:8+9+13+11+9=50,由右图可知,“1分钟仰卧起坐”测试中第三成绩段(从左到右)即36-38个的女生人数为13,即可得出人数的比值,进而得出圆心角的度数.
(2)根据前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,利用条形图高度之比等于人数之比,求出即可.
(3)从左图,求得该校九年级全体女生优秀等级人数训练前的人数.由图,求得该校九年级全体女生优秀等级人数训练后的人数,然后便可估算出该校九年级全体女生优秀等级人数训练后比训练前增加的人数.
(2)根据前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,利用条形图高度之比等于人数之比,求出即可.
(3)从左图,求得该校九年级全体女生优秀等级人数训练前的人数.由图,求得该校九年级全体女生优秀等级人数训练后的人数,然后便可估算出该校九年级全体女生优秀等级人数训练后比训练前增加的人数.
解答:解:(1)∵“1分钟仰卧起坐”的总人数:8+9+13+11+9=50,由图可知,“1分钟仰卧起坐”测试中第三成绩段(从左到右)即36-38个的女生人数为13人,
∴第三成绩段(从左到右)的圆心角为:
×360°=93.6°,
故答案为:93.6.
(2)∵前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,
∴第二成绩段有2×4=8人,第三成绩段有2×5=10人,第四成绩段有2×5=10人.
(3)依题意知:500×
-500×
=100(人).
答:估计该校九年级全体女生训练后优秀等级增加的人数为100人.
∴第三成绩段(从左到右)的圆心角为:
| 13 |
| 50 |
故答案为:93.6.
(2)∵前四段成绩(从左到右)条形图的高度之比依次为1:4:5:5,且第一成绩段有2人,
∴第二成绩段有2×4=8人,第三成绩段有2×5=10人,第四成绩段有2×5=10人.
(3)依题意知:500×
| 30 |
| 50 |
| 20 |
| 50 |
答:估计该校九年级全体女生训练后优秀等级增加的人数为100人.
点评:本题考查了条形统计图的运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.

练习册系列答案
相关题目
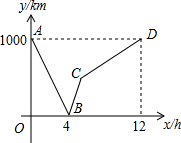 (2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )
(2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )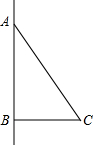 (2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是
(2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是