题目内容
如图①,抛物线y=ax2+bx+5交x轴于A、B,交y轴于C,抛物线的顶点D的横坐标为4,OA•OC=OB.
(1)求抛物线的解析式;
(2)如图②,若P为抛物线上一动点,PQ∥y轴交直线l:y= +9于点Q,以PQ为对角线作矩形且使得矩形的一边在直线l上,问是否存在这样一点P使得矩形的面积最小?若存在,求其最小值;若不存在,请说明理由
+9于点Q,以PQ为对角线作矩形且使得矩形的一边在直线l上,问是否存在这样一点P使得矩形的面积最小?若存在,求其最小值;若不存在,请说明理由
(3)如图③,将直线向下平移m个单位(m>9),设平移后的直线交抛物线于M、N两点(点M在点N左边),M关于原点的对称点为M′,连接M′N,问M′N在x轴上的正投影是否为定值?若为定值,求其值;若不是定值,请说明理由.

解:(1)令x=0,则y=5,
所以,点C的坐标为(0,5),OC=5,
∵OA•OC=OB,
∴5OA=OB,
∴-5xA=xB,①
∵抛物线的顶点D的横坐标为4,
∴ =4,②
=4,②
①、②联立解得,xA=-2,xB=10,
∴点A(-2,0),B(10,0),
∵抛物线y=ax2+bx+5交x轴于A、B,
∴ ,
,
解得 ,
,
所以,抛物线解析式为y=- x2+2x+5;
x2+2x+5;
(2)∵以PQ为对角线的矩形的一边在直线l:y= x+9上,
x+9上, =5,
=5,
∴矩形的长、宽分别为 PQ,
PQ, PQ,
PQ,
∴矩形的面积为 PQ•
PQ• PQ=
PQ= PQ2,
PQ2,
∵点P在抛物线y=- x2+2x+5上,点Q在直线y=
x2+2x+5上,点Q在直线y= x+9上,
x+9上,
∴PQ=xQ-xP= x+9-(-
x+9-(- x2+2x+5)=
x2+2x+5)= x2-
x2- x+4=
x+4= (x2-5x+
(x2-5x+ )-
)- +4=
+4= (x-
(x- )2+
)2+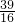 ,
,
∴当x= 时,PQ有最小值为
时,PQ有最小值为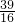 ,
,
故矩形面积的最小值为 ×(
×(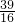 )2=
)2= ;
;
(3)是定值5.
理由如下:设M′N在x轴上的正投影为EF,则EF等于点N的横坐标减去点M′的横坐标,
∵直线y= x+9向下平移m个单位,
x+9向下平移m个单位,
∴平移后的直线解析式为y= x+9-m,
x+9-m,
联立 ,
,
消掉y得, x2-
x2- x+4-m=0,
x+4-m=0,
∵点M与点M′关于原点对称,
∴点M′的横坐标与点M的横坐标互为相反数,
∴EF=- =5,是定值.
=5,是定值.
分析:(1)根据抛物线求出点C的坐标为(0,5),从而得到OC的长度是5,然后得到点B的横坐标是点A的横坐标的5倍,再根据顶点的横坐标列式求出点A、B的坐标,然后利用待定系数法求二次函数解析式解答即可;
(2)根据直线l的解析式表示出矩形的长与宽与PQ的关系,然后表示出矩形的面积,再根据直线与抛物线的解析式表示出PQ,然后根据二次函数的最值问题求出PQ,再代入进行计算即可得解;
(3)先表示出M′N在x轴上的正投影,再根据向下平移纵坐标减表示出平移后的直线解析式,然后与抛物线联立,消掉y得到关于x的一元二次方程,再根据关于原点对称的点的横坐标互为相反数用点M的坐标表示出点M′的横坐标,然后根据正投影的定义,表示出点M′N的横坐标的差值即可得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,矩形的面积,二次函数的最值问题,联立两函数解析式求交点,根与系数的关系,综合性较强,(1)求出点A、B的关系式,(2)根据直线用PQ表示出矩形的长与宽,(3)根据点M、M′的横坐标的关系利用根与系数的关系判断是解题的关键.
所以,点C的坐标为(0,5),OC=5,
∵OA•OC=OB,
∴5OA=OB,
∴-5xA=xB,①
∵抛物线的顶点D的横坐标为4,
∴
 =4,②
=4,②①、②联立解得,xA=-2,xB=10,
∴点A(-2,0),B(10,0),
∵抛物线y=ax2+bx+5交x轴于A、B,
∴
 ,
,解得
 ,
,所以,抛物线解析式为y=-
 x2+2x+5;
x2+2x+5;(2)∵以PQ为对角线的矩形的一边在直线l:y=
 x+9上,
x+9上, =5,
=5,
∴矩形的长、宽分别为
 PQ,
PQ, PQ,
PQ,∴矩形的面积为
 PQ•
PQ• PQ=
PQ= PQ2,
PQ2,∵点P在抛物线y=-
 x2+2x+5上,点Q在直线y=
x2+2x+5上,点Q在直线y= x+9上,
x+9上,∴PQ=xQ-xP=
 x+9-(-
x+9-(- x2+2x+5)=
x2+2x+5)= x2-
x2- x+4=
x+4= (x2-5x+
(x2-5x+ )-
)- +4=
+4= (x-
(x- )2+
)2+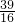 ,
,∴当x=
 时,PQ有最小值为
时,PQ有最小值为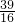 ,
,故矩形面积的最小值为
 ×(
×(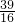 )2=
)2= ;
;(3)是定值5.
理由如下:设M′N在x轴上的正投影为EF,则EF等于点N的横坐标减去点M′的横坐标,
∵直线y=
 x+9向下平移m个单位,
x+9向下平移m个单位,∴平移后的直线解析式为y=
 x+9-m,
x+9-m,联立
 ,
,消掉y得,
 x2-
x2- x+4-m=0,
x+4-m=0,∵点M与点M′关于原点对称,
∴点M′的横坐标与点M的横坐标互为相反数,
∴EF=-
 =5,是定值.
=5,是定值.分析:(1)根据抛物线求出点C的坐标为(0,5),从而得到OC的长度是5,然后得到点B的横坐标是点A的横坐标的5倍,再根据顶点的横坐标列式求出点A、B的坐标,然后利用待定系数法求二次函数解析式解答即可;
(2)根据直线l的解析式表示出矩形的长与宽与PQ的关系,然后表示出矩形的面积,再根据直线与抛物线的解析式表示出PQ,然后根据二次函数的最值问题求出PQ,再代入进行计算即可得解;
(3)先表示出M′N在x轴上的正投影,再根据向下平移纵坐标减表示出平移后的直线解析式,然后与抛物线联立,消掉y得到关于x的一元二次方程,再根据关于原点对称的点的横坐标互为相反数用点M的坐标表示出点M′的横坐标,然后根据正投影的定义,表示出点M′N的横坐标的差值即可得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,矩形的面积,二次函数的最值问题,联立两函数解析式求交点,根与系数的关系,综合性较强,(1)求出点A、B的关系式,(2)根据直线用PQ表示出矩形的长与宽,(3)根据点M、M′的横坐标的关系利用根与系数的关系判断是解题的关键.

练习册系列答案
相关题目
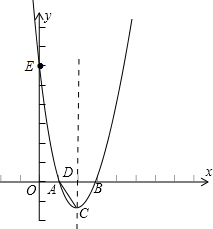 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=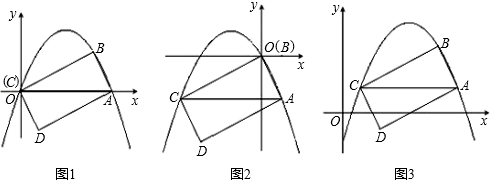
 如图,将抛物线
如图,将抛物线