题目内容
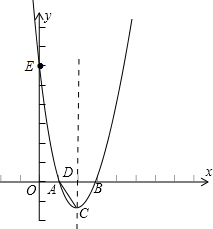已知二次函数的图象是经过点A（1，0），B（3，0），E（0，6）三点的一条抛物线．（1）求这条抛物线的解析式；
（2）如图，设抛物线的顶点为C，对称轴交x轴于点D，在y轴正半轴上有一点P，且以A、O、P为顶点的三角形与△ACD相似，求P点的坐标．
分析：（1）由抛物线与x轴的两交点坐标（1，0）（3，0）设出解析式y=a（x-1）（x-3），再把（0，6）代入求解a值即可．
（2）由抛物线的解析式先确定C、D两点坐标，再由△AOP∽△ACD，求得P点坐标．
（2）由抛物线的解析式先确定C、D两点坐标，再由△AOP∽△ACD，求得P点坐标．
解答：解：（1）设抛物线解析式为：y=a（x-1）（x-3），
∵过E（0，6），∴6=a×3，
∴a=2，
∴抛物线的解析式为：y=2x2-8x+6．
（2）y=2x2-8x+6=2（x2-4x+3）-2=2（x-2）2-2，
∴C（2，-2），对称轴直线x=2，D（2，0）．
△ACD为直角三角形，AD=1，CD=2，OA=1．
当△AOP∽△ACD时，
=
，
=
，∴OP=2．
∵P在y轴正半轴上，∴P（0，2）．
当△PAO∽△ACD时，
=
，
=
，OP=
，
P在y轴正半轴上，∴P（0，
）．
∵过E（0，6），∴6=a×3，
∴a=2，
∴抛物线的解析式为：y=2x2-8x+6．
（2）y=2x2-8x+6=2（x2-4x+3）-2=2（x-2）2-2，
∴C（2，-2），对称轴直线x=2，D（2，0）．
△ACD为直角三角形，AD=1，CD=2，OA=1．
当△AOP∽△ACD时，
| OA |
| AD |
| OP |
| CD |
| 1 |
| 1 |
| OP |
| 2 |
∵P在y轴正半轴上，∴P（0，2）．
当△PAO∽△ACD时，
| OA |
| CD |
| OP |
| AD |
| 1 |
| 2 |
| OP |
| 1 |
| 1 |
| 2 |
P在y轴正半轴上，∴P（0，
| 1 |
| 2 |
点评：本题考查了二次函数解析式的求法以及数形结合的思想．
练习册系列答案
相关题目
已知二次函数的图象是经过点A（1，0），B（3，0），E（0，6）三点的一条抛物线．
