题目内容
 如图,将抛物线y=-
如图,将抛物线y=-| 1 |
| 2 |
| 1 |
| 2 |
分析:根据点O与点A的坐标求出平移后的抛物线的对称轴,然后求出点C的坐标,过点C作CD⊥y轴于点D,根据抛物线的对称性可知阴影部分的面积等于四边形CDOE的面积,然后求解即可.
解答: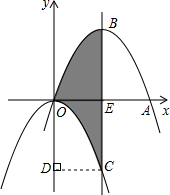 解:∵抛物线平移后经过原点O和点A(6,0),
解:∵抛物线平移后经过原点O和点A(6,0),
∴平移后的抛物线对称轴为x=3,
当x=3时,y=-
×32=-
,
∴点C的坐标是(3,-
),
过点C作CD⊥y轴于点D,根据抛物线的对称性可知,阴影部分的面积等于矩形CDOE的面积,
∴S=3×|-
|=
.
故选C.
 解:∵抛物线平移后经过原点O和点A(6,0),
解:∵抛物线平移后经过原点O和点A(6,0),∴平移后的抛物线对称轴为x=3,
当x=3时,y=-
| 1 |
| 2 |
| 9 |
| 2 |
∴点C的坐标是(3,-
| 9 |
| 2 |
过点C作CD⊥y轴于点D,根据抛物线的对称性可知,阴影部分的面积等于矩形CDOE的面积,
∴S=3×|-
| 9 |
| 2 |
| 27 |
| 2 |
故选C.
点评:本题综合考查了二次函数的问题,根据二次函数的性质求出平移后的抛物线的对称轴的解析式,并对阴影部分的面积进行转换是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
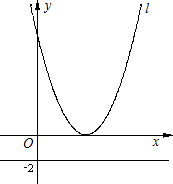 如图,将抛物线y=x2沿x轴正方向平移3个单位得到抛物线l,直线y=-2.
如图,将抛物线y=x2沿x轴正方向平移3个单位得到抛物线l,直线y=-2. 上,点C是抛物线与y轴的交点,且OC=3OA.
上,点C是抛物线与y轴的交点,且OC=3OA.
 如图,将抛物线y=-
如图,将抛物线y=-