题目内容
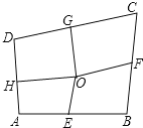
【题目】如图,四边形ABCD中,E.F.G.H依次是各边的中点,O是四边形ABCD内一点,若四边形AEOH.四边形BFOE.四边形CGOF的面积分别为10.12.14,则四边形DHOG的面积=______.
【答案】12
【解析】
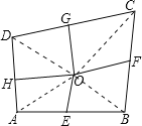
连接OC,OB,OA,OD,易证S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,S△OAE=S△OBE,所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,所以可以求出S四边形DHOG.
解:连接OC,OB,OA,OD,
∵E.F.G.H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,
同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,
∵S四边形AEOH=10,S四边形BFOE=12,S四边形CGOF=14,
∴10+14=12+S四边形DHOG,
解得,S四边形DHOG=12.
故答案为:12.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.