题目内容
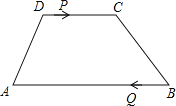
【题目】如图,在正方形![]() 中,点
中,点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上.
上.
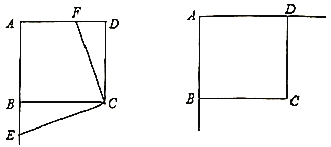
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,则
,则![]() 是否成立?若成立,请给出证明,若不成立,请画图说明.
是否成立?若成立,请给出证明,若不成立,请画图说明.
【答案】(1)证明见解析 (2)答案见解析
【解析】
(1)首先由正方形的性质得CB=CD,利用全等三角形的ASA判定得△BCE和△DCF全等,由全等三角形的性质得出结论;
(2)根据正方形的性质和全等三角形的判定和性质进行证明即可.
(1)证明:∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]() ,∴
,∴![]()
∵![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]() .
.
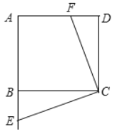
(2)若![]() ,则
,则![]() 不一定成立
不一定成立
当点![]() 在线段
在线段![]() 上,且点
上,且点![]() 在
在![]() 延长线上或当点
延长线上或当点![]() 在
在![]() 延长线上,且点
延长线上,且点![]() 在线段
在线段![]() 上时
上时![]() 成立.
成立.
证明如下:
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]() ,
,
∴![]()
∵img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/07/ca3f59ae/SYS202011270752436822811761_DA/SYS202011270752436822811761_DA.009.png" width="56" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
∴![]() ,
,
∴![]() ,
,![]()
∴![]()
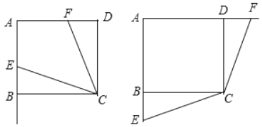
当点![]() 在线段
在线段![]() 上,且点
上,且点![]() 在线段
在线段![]() 上或当点
上或当点![]() 在线段
在线段![]() 延长线上,且点
延长线上,且点![]() 在
在![]() 延长线上时,
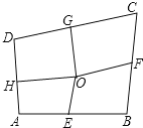
延长线上时,![]() 不成立,如下图所示
不成立,如下图所示

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目