Question

【题目】已知为原点，点及在第一象限的动点，且，设的面积为.

（1）求关于的函数解析式；

（2）求的取值范围；

（3）当时，求点坐标；

（4）画出函数的图象.

Answer 1

【答案】（1）S＝4x＋48；（2）0＜x＜12；（3）P（9，3）；（4）见解析.

【解析】

（1）根据三角形的面积公式即可得出结论；

（2）根据（1）中函数关系式及点P在第一象限即可得出结论；

（3）把S＝12代入（1）中函数关系即可得出x的值，进而得出y的值；

（4）利用描点法画出函数图象即可．

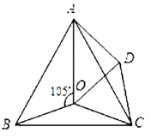
解：（1）∵A点和P点的坐标分别是（8，0）、（x，y），

∴S＝×8×y＝4y．

∵x＋y＝12，

∴y＝12x．

∴S＝4（12x）＝484x，

∴所求的函数关系式为：S＝4x＋48；

（2）由（1）得S＝4x＋48＞0，

解得：x＜12；

又∵点P在第一象限，

∴x＞0，

综上可得x的取值范围为：0＜x＜12；

（3）∵S＝12，

∴4x＋48＝12，

解得x＝9．

∵x＋y＝12，

∴y＝129＝3，

即P（9，3）；

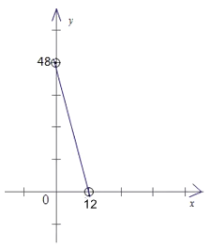
（4）∵函数解析式为S＝4x＋48，

∴函数图象是经过点（12，0）（0，48）但不包括这两点的线段．

所画图象如图：