题目内容
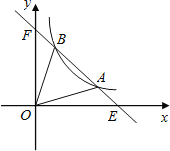
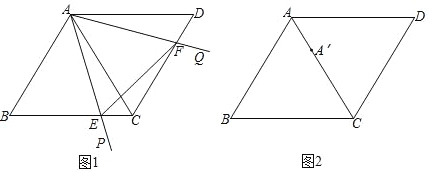
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
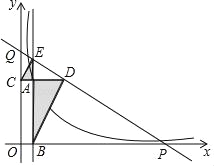
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
【答案】(1)AE=AF;(2)存在,S△AEF的最小值为![]() ;(3)满足条件的EC的值为6或10.
;(3)满足条件的EC的值为6或10.
【解析】
(1)结论:AE=AF.只要证明△ACE≌△ADF即可解决问题.
(2)证明△AEF为等边三角形,故只有边长最小时,△AEF的面积才最小,当AP⊥BC时,AE为最小.
(3)分两种情形分别求解即可解决问题:①如图2中,当等E在CB的延长线上时.②如图3中,当点E在BC的延长线上时.
解:(1)结论:AE=AF.
理由:如图1中,
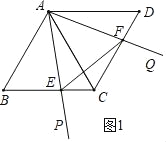
∵四边形ABCD是菱形,
∴AB=BC=CD=AD
∵∠ABC=60°,
∴∠ACE=∠ADF=60°,
∴AC=AD,
又∵∠PAQ=60°,
∴∠ACE=∠ADF=∠CAD=60°,AC=AD,
∴∠CAE=∠DAF,
∴△ACE≌△ADF(ASA),
∴AE=AF.
(2)存在.
理由:如图1中,由(1)得AE=AF,∠PAQ=60°
∴△AEF为等边三角形,
故只有边长最小时,△AEF的面积才最小,
∴当AP⊥BC时,AE为最小,
∵AB=6,
此时AE=3![]() ,则S△AEF的最小值为
,则S△AEF的最小值为![]() .
.
(3)①如图2中,当等E在CB的延长线上时,作A′H⊥BC于H.
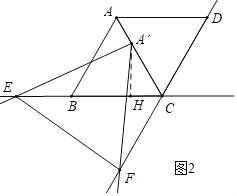
由题意菱形ABCD的面积=2×![]() ×62=18
×62=18![]() ,
,
∵S△A′EF:S菱形ABCD=19:18,
∴S△AEF=19![]() ,
,
∵△A′EF是等边三角形,
∴![]() ×A′E2=19
×A′E2=19![]() ,
,
∴A′E2=76,
在Rt△A′CH中,∵CA′=4,∠A′CH=60°,
∴CH=![]() ×4=2,A′H=2
×4=2,A′H=2![]() ,
,
∴EH=![]() =8,
=8,
∴CE=EH+CH=8+2=10.
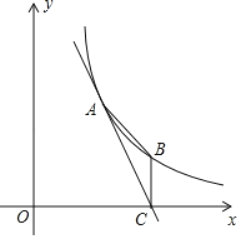
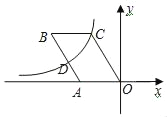
②如图3中,当点E在BC的延长线上时,作A′H⊥BC于H.
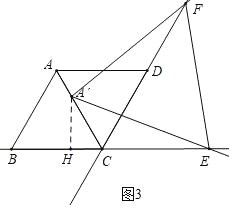
同法可证EH=8,可得EC=EH=CH=8﹣2=6,
综上所述,满足条件的EC的值为6或10.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |