题目内容
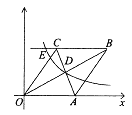
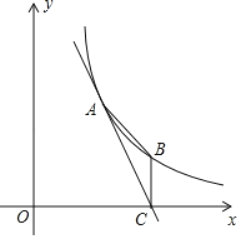
【题目】如图，反比例函数y＝
（x＞0）过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线交反比例函数图象于点B．
（1）求反比例函数和直线AC的解析式；
（2）求△ABC的面积；
（3）在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，请直接写出符合条件的所有D点的坐标．
【答案】（1）y＝
；y＝﹣
x+8；（2）B（6，2）；△ABC的面积＝3；（3）（3，2）或（3，6）或（9，﹣2）．
【解析】
（1）把点A的坐标代入反比例函数即可求出k，再把点A和点C的坐标代入一次函数中即可求出解析式；
（2）由题意BC⊥x轴，且点B在反比例函数上，可求出点B的坐标，从而求出△ABC的面积；
（3）根据平行四边形的性质求得点D的坐标，注意分三种情况讨论.
解：（1）把点A（3，4）代入y＝
（x＞0），得
k＝xy＝3×4＝12，
故该反比例函数解析式为：y＝；
把A（3，4），C（6，0）代入y＝mx+n中，
可得：
，
解得：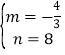
，
所以直线AC的解析式为：y＝﹣x+8；
（2）∵点C（6，0），BC⊥x轴，
∴把x＝6代入反比例函数y＝，得
y＝
＝2．
则B（6，2）．
所以△ABC的面积＝
；
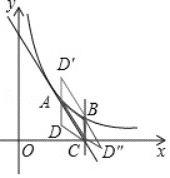
（3）①如图，当四边形ABCD为平行四边形时，AD∥BC且AD＝BC，
∵A（3，4）、B（6，2）、C（6，0），
∴点D的横坐标为3，yA﹣yD＝yB﹣yC即4﹣yD＝2﹣0，故yD＝2，
所以D（3，2）；
②如图，当四边形ACBD′为平行四边形时，AD′∥CB且AD′＝CB，
∵A（3，4）、B（6，2）、C（6，0），
∴点D的横坐标为3，yD′﹣yA＝yB﹣yC即yD﹣4＝2﹣0，故yD′＝6．
所以D′（3，6）．
③如图，当四边形ACD″B为平行四边形时，AC＝BD″且AC∥BD″．
∵A（3，4）、B（6，2）、C（6，0），
∴xD″﹣xB＝xC﹣xA即xD″﹣6＝6﹣3，故xD″＝9．
yD″﹣yB＝yC﹣yA即yD″﹣2＝0﹣4，故yD″＝﹣2．
所以D″（9，﹣2）．
综上所述，符合条件的点D的坐标是：（3，2）或（3，6）或（9，﹣2）．
