题目内容
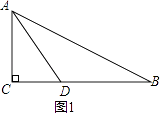
【题目】在Rt△ABC中，∠C=90°，BC=8cm，AC=6cm，在射线BC上一动点D，从点B出发，以2厘米每秒的速度匀速运动，若点D运动t秒时，以A、D、B为顶点的三角形恰为等腰三角形，则所用时间t为秒．
【答案】
，5，8
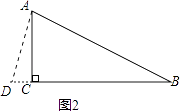
【解析】解：①如图1，当AD=BD时，在Rt△ACD中，根据勾股定理得到：AD2=AC2+CD2 ， 即BD2=（8﹣BD）2+62 ，
解得，BD= 
（cm），
则t= 
= （秒）；
②如图2，当AB=BD时．
在Rt△ABC中，根据勾股定理得到：
AB= 
= 
=10，则t= 
=5（秒）；
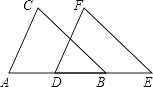
③如图3，当AD=AB时，BD=2BC=16，则t= 
=8（秒）；
综上所述，t的值可以是： ，5，8；
故答案是： ，5，8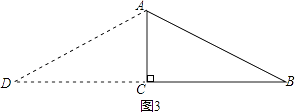
当△BCD为等腰三角形时应分当D是顶角顶点，当B是顶角顶点，当A是顶角的顶点三种情况进行讨论，利用勾股定理求得BD的长，从而求解．
练习册系列答案
相关题目
【题目】“节能环保，低碳生活”是我们倡导的一种生活方式，某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台，三种家电的进价和售价如表所示：
价格 | 进价 | 售价 |
电视机 | 5000 | 5500 |
洗衣机 | 2000 | 2160 |
空 调 | 2400 | 2700 |
（1）在不超出现有资金的前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的3倍．请问商场有哪几种进货方案？
（2）在“2012年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动．在（1）的条件下，若三种电器在活动期间全部售出，商家预估最多送出多少张？
