题目内容
【题目】综合与探究
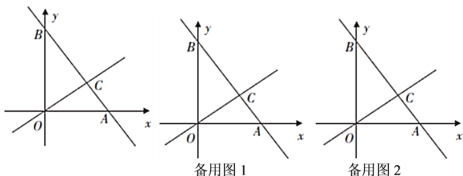
如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在
在![]() 轴上运动.
轴上运动.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)求使![]() 的周长最小时点
的周长最小时点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?如果存在,直接写出点
为直角边的直角三角形?如果存在,直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)P
;(2)P![]() ;(3)满足条件的点
;(3)满足条件的点![]() ,
,![]()
【解析】
(1)设直线![]() 的函数表达式为
的函数表达式为![]() ,将
,将![]() ,
,![]() 代入连立方程组求解即可;
代入连立方程组求解即可;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,即
最小,即![]() 的周长最小,设直线
的周长最小,设直线![]() 的函数表达式为
的函数表达式为![]() ,代入C点坐标求得函数关系式,令
,代入C点坐标求得函数关系式,令![]() ,即可得到P点坐标.
,即可得到P点坐标.
(3)设CP的函数关系式为y=mx+n,当CP垂直AB时,∠PCA=90°,求得m的值,将m和C点坐标代入即可求得CP的函数关系式,即可求得P点坐标,当∠PAB=90°同理也可求解.
解:(1)设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() ,
,![]() 在直线
在直线![]() 上,
上,
![]() ,
,
解,得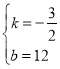 .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
(2)如图,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,
![]()
![]()
连接![]() 交
交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,即
最小,即![]() 的周长最小;
的周长最小;
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() ,
,
![]() ,
,
解得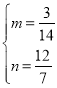
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]()
令![]() ,得
,得![]() ,
,
![]()

(3)设CP的函数关系式为y=mx+n
当CP垂直AB时,∠PCA=90°,
kab×m=-1,
∴m=![]() ,
,
将m=![]() ,
,![]() 代入y=mx+n可得
代入y=mx+n可得
n=-1,
∴CP:![]()
当x=0时,y=-1,
即P1的坐标为![]() ,
,
设CA的函数关系式为y=cx+d,
当CA垂直AB时,∠PAB=90°,
kab×c=-1,
∴c=![]() ,
,
将c=![]() ,
,![]() 代入y=cx+d可得
代入y=cx+d可得
d=![]() ,
,
∴CA:![]()
当x=0时,y=![]() -1,
-1,
即P2的坐标为![]() ,
,
∴满足条件的点![]() ,
,![]()

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案【题目】“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元
元![]() 公里计算,耗时费按
公里计算,耗时费按![]() 元
元![]() 分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:
分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:

平均速度(公里/时) | 里程数(公里) | 车费(元) | |
甲乘客 |
|
|
|
乙乘客 |
|
|
|
(1)求![]() ,
,![]() 的值;
的值;
(2)如果你采用“滴滴出行”的打车方式,保持平均车速![]() 公里
公里![]() 时,行驶了
时,行驶了![]() 公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.
公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.