题目内容
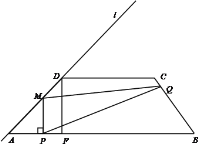
【题目】如图,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直线l经过A,D两点,且sin∠DAB=
, CD=7.直线l经过A,D两点,且sin∠DAB=![]() . 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的![]() ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
【答案】(1)5;(2)S=﹣5t2+14t(0<t≤1)(3)不存在,理由见解析;(4)t=![]() 或t=
或t=![]()
【解析】
试题(1)利用梯形性质确定点D的坐标,利用sin∠DAB=![]() 特殊三角函数值,得到△AOD为等腰直角三角形,求出梯形的高,然后利用勾股定理求出BC有长;
特殊三角函数值,得到△AOD为等腰直角三角形,求出梯形的高,然后利用勾股定理求出BC有长;
(2)当0<t≤1时,S=![]() ×2t×(14﹣5t)=﹣5t2+14t;
×2t×(14﹣5t)=﹣5t2+14t;
(3)在(2)的条件下,不存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的
(4)△QMN为等腰三角形的情形有两种,需要分类讨论,避免漏解.
试题解析:(1)5
(2)当0<t≤1时,S=![]() ×2t×(14﹣5t)=﹣5t2+14t
×2t×(14﹣5t)=﹣5t2+14t
(3)梯形ABCD的面积为42
﹣5t2+14t=![]()
![]() 42程无解,所以△MPQ的面积不能为梯形ABCD的
42程无解,所以△MPQ的面积不能为梯形ABCD的![]() 。
。
(4)△QMN为等腰三角形,有两种情形:
①如图4所示,点M在线段NM的右侧上
 ,
,
MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,MN=DM=2t-4,
由MN=MQ,得16-7t=2t-4,解得t=![]() ;
;
②如图5所示,当Q在MN的左侧时,5t-5+(2t-4)-7=(2t-4)+4-4,

解得:t=![]() .
.
故当t=![]() 或t=
或t=![]() 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.
考点: 一次函数综合题.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案